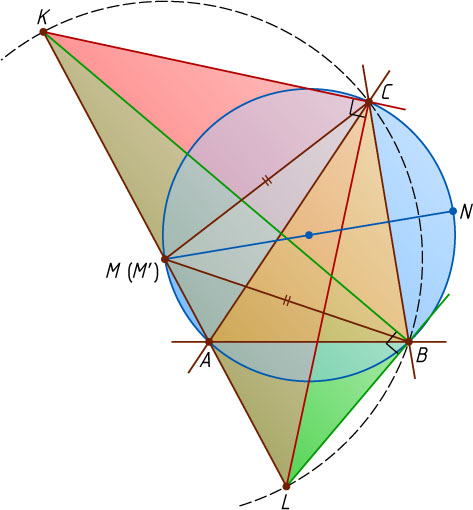
3357. Дан треугольник ABC
и окружность, описанная вокруг него. K
— точка пересечения биссектрис внутреннего угла B
и внешнего угла C
, L
— точка пересечения биссектрис внутреннего угла C
и внешнего угла B
; M
— середина отрезка KL
. Докажите, что M
— середина дуги BAC
.
Решение. Биссектрисы двух внешних и третьего внутреннего углов треугольника пересекаются в одной точке (центре вневписанной окружности треугольника). Поэтому AK
и AL
— биссектрисы вертикальных углов — внешних углов при вершине A
треугольника ABC
. Значит, прямая KL
проходит через вершину A
.
Пусть M'
— отличная от A
точка пересечения окружности с прямой KL
, а N
— середина дуги BC
, не содержащей точку M'
. Тогда AN
— биссектриса угла BAC
, а так как \angle M'AN=90^{\circ}
(как угол между биссектрисами смежных углов), то M'N
— диаметр окружности, поэтому M'
— середина дуги BAC
, а M'N
— серединный перпендикуляр к хорде BC
.
Биссектрисы смежных углов взаимно перпендикулярны, поэтому из точек B
и C
отрезок KL
виден под прямым углом. Значит, эти точки лежат на окружности с диаметром KL
. Серединный перпендикуляр к хорде BC
этой окружности пересекает её диаметр KL
в точке M'
, поэтому M'
— центр окружности, т. е. середина KL
. Следовательно, точки M'
и M
совпадают. Что и требовалось доказать.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1976, 9 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 76.24.
