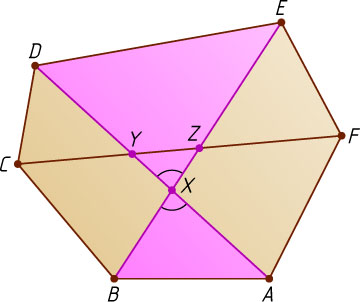
3359. Дан выпуклый шестиугольник, каждая диагональ которого, соединяющая противоположные вершины, делит его площадь пополам. Докажите, что эти диагонали пересекаются в одной точке.
Решение. Пусть диагональ AD
выпуклого шестиугольника ABCDEF
пересекается с диагоналями BE
и CF
в точках X
и Y
соответственно, а диагонали BE
и CF
пересекаются в точке Z
, причём точка X
лежит между A
и Y
, а Z
— между E
и X
. Тогда
S_{\triangle ABX}=S_{\triangle XDE},~S_{\triangle BCZ}=S_{\triangle ZEF},~S_{\triangle CDY}=S_{\triangle YAF}
(например, площадь каждого из треугольников ABX
и XDE
равна разности половины площади данного шестиугольника и четырёхугольника BCDX
). Поэтому
AX\cdot BX=DX\cdot EX\gt DY\cdot EZ,
FZ\cdot EZ=CZ\cdot BZ\gt BX\cdot CY,
CY\cdot DY=AY\cdot FY\gt AX\cdot FZ,
значит,
(AX\cdot BX)(FZ\cdot EZ)(CY\cdot DY)\gt(DY\cdot EZ)(BX\cdot CY)(AX\cdot FZ),
что невозможно. Следовательно, отрезки AD
, BE
и CF
пересекаются в одной точке. Аналогично для остальных случаев.
Источник: Польские математические олимпиады. — 1965, задача 5
Источник: Страшевич С., Бровкин Е. Польские математические олимпиады. — М.: Мир, 1978. — № 101, с. 25
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1978, 10 кл.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 6.55, с. 157
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 6.51, с. 156
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 78.27.
Источник: Датские математические олимпиады. — 1985
Источник: Журнал «Crux Mathematicorum». — 1988, № 4, задача 4 (1986, с. 4), с. 104
