3373. Боковые стороны трапеции лежат на перпендикулярных прямых. Найдите площадь четырёхугольника с вершинами в серединах диагоналей и в серединах оснований трапеции, если её боковые стороны равны a
и b
.
Ответ. \frac{ab}{4}
.
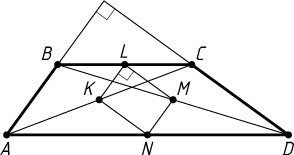
Решение. Пусть K
и M
— середины диагоналей соответственно AC
и BD
трапеции ABCD
, а L
и N
— середины оснований соответственно BC
и AD
, причём AB\perp CD
, AB=a
и CD=b
.
Отрезки KL
и MN
— средние линии треугольников ABC
и ABD
с общим основанием AB
, поэтому KL\parallel AB
, KL=\frac{1}{2}AB=\frac{1}{2}a
, MN\parallel AB
, MN=\frac{1}{2}AB=\frac{1}{2}a
. Аналогично, KN=LM=\frac{1}{2}CD=\frac{1}{2}b
. Противоположные стороны четырёхугольника KLMN
попарно равны, значит, это параллелограмм, а так как его стороны соответственно параллельны боковым сторонам AB
и CD
трапеции ABCD
, то KLMN
— прямоугольник. Его площадь равна произведению соседних сторон, причём KL=\frac{1}{2}a
и LM=\frac{1}{2}b
. Следовательно,
S_{KLMN}=KL\cdot LM=\frac{1}{2}AB\cdot\frac{1}{2}CD=\frac{1}{2}a\cdot\frac{1}{2}b=\frac{1}{4}ab.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.20, с. 31
