3374. Дан треугольник ABC
, AA_{1}
, BB_{1}
и CC_{1}
— его биссектрисы. Известно, что величины углов A
, B
и C
относятся как 4:2:1
. Докажите, что A_{1}B_{1}=A_{1}C_{1}
.
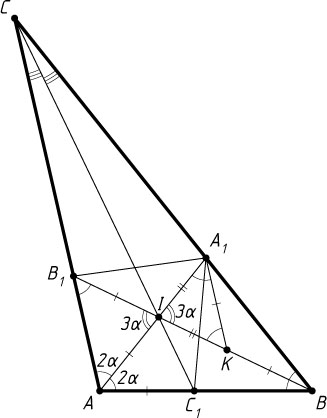
Решение. Первый способ. Пусть I
— точка пересечения биссектрис треугольника ABC
(рис. 1). Положим \angle ACB=\alpha
. Тогда \angle ABC=2\alpha
, \angle CAB=4\alpha
, а следовательно, \alpha+2\alpha+4\alpha=180^{\circ}
, т. е.
7\alpha=180^{\circ},~\angle CC_{1}A=180^{\circ}-\angle CAB-\angle C_{1}CA=\frac{5\alpha}{2},
\angle C_{1}IA=180^{\circ}-\angle IC_{1}A-\angle C_{1}AI=\frac{5\alpha}{2},
а значит, IA=C_{1}A
,
\angle AB_{1}I=180^{\circ}-\angle BAB_{1}-\angle B_{1}BA=2\alpha=\angle IAB_{1},
а значит, IA=IB_{1}
;
\angle BIA_{1}=\angle AIB_{1}=180^{\circ}-\angle IAB_{1}-\angle IB_{1}A=3\alpha,~\angle A_{1}BA=2\alpha=\angle A_{1}AB,
следовательно, AA_{1}=BA_{1}
и \angle AA_{1}B=3\alpha
, а значит, BA_{1}=BI
.
Отметим на отрезке BI
точку K
так, чтобы угол KA_{1}A
был равен 2\alpha
. Тогда
\angle A_{1}KI=180^{\circ}-\angle KA_{1}I-\angle A_{1}IK=2\alpha,
а значит, A_{1}I=KI
и
\angle BKA_{1}=\angle KA_{1}I+\angle KIA_{1}=5\alpha,
следовательно,
\angle BA_{1}K=180^{\circ}-\angle A_{1}BK-\angle BKA_{1}=\alpha,
а следовательно, BK=A_{1}K
.
Докажем, что треугольник KA_{1}B_{1}
равен треугольнику AC_{1}A_{1}
:
A_{1}K=BK=BI-KI=BA_{1}-KI=A_{1}A-KI=A_{1}A-A_{1}I=AI=AC_{1},
KB_{1}=KI+IB_{1}=A_{1}I+IB_{1}=A_{1}I+IA=A_{1}A,
\angle A_{1}KB_{1}=2\alpha=\angle C_{1}AA_{1},
значит, треугольники равны по двум сторонам и углу между ними, а следовательно, A_{1}B_{1}=A_{1}C_{1}
.
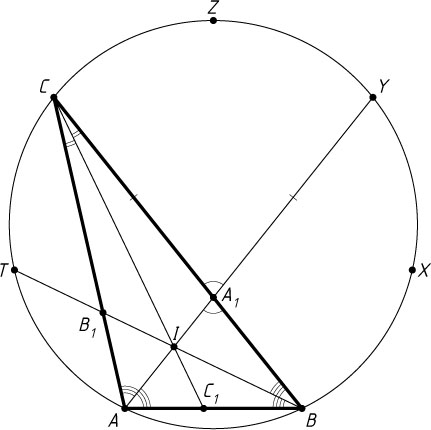
Второй способ. Опишем вокруг треугольника ABC
окружность (рис. 2). Углы нашего треугольника равны \frac{4\cdot180^{\circ}}{7}
, \frac{2\cdot180^{\circ}}{7}
и \frac{180^{\circ}}{7}
, поэтому, разделив окружность на 7 равных дуг, начиная с точки A
, мы получим вписанный в окружность правильный семиугольник ABXYZCT
.
Так как AA_{1}
— биссектриса угла BAC
, то она проходит через точку Y
— середину дуги BC
. Аналогично, BB_{1}
— биссектриса угла ABC
, а значит, проходит через точку T
— середину дуги AC
.
Из симметрии очевидно, что BA_{1}=AA_{1}
и YA_{1}=CA_{1}
, а следовательно при повороте вокруг точки A_{1}
на угол BA_{1}A
точка B
перейдёт в точку A
, а точка C
— в точку Y
(так как \angle BA_{1}A=\angle CA_{1}Y
). Кроме того, прямая BA
перейдёт в прямую AC
(так как \angle A_{1}BA=\frac{2\cdot180^{\circ}}{7}=\angle A_{1}AC
), а прямая C_{1}C
— в прямую B_{1}Y
(так как \angle BCC_{1}=\frac{180^{\circ}}{14}=\angle AYB_{1}
, первое равенство верно, ввиду того, что CC_{1}
— биссектриса угла ACB
, второе — ввиду того, что YB_{1}
— биссектриса угла AYT
из симметрии), а следовательно, точка пересечения прямых BA
и CC_{1}
(т. е. точка C_{1}
) перейдёт в точку пересечения прямых AC
и YB_{1}
(т. е. в точку B_{1}
). Но тогда отрезок A_{1}C_{1}
перейдёт в отрезок A_{1}B_{1}
, т. е. A_{1}C_{1}=A_{1}B_{1}
.
Автор: Токарев С. И.
Источник: Турнир городов. — 2005-2006, XXVII, осенний тур, старшие классы, основной вариант

