3377. Две окружности пересекаются в точках A
и B
. Через точку A
проведены диаметры AC
и AD
этих окружностей. Найдите расстояние между центрами окружностей, если BC=a
и BD=b
.
Ответ. \frac{a+b}{2}
или \frac{|a-b|}{2}
.
Решение. Пусть O_{1}
— центр окружности с диаметром AC
, O_{2}
— центр окружности с диаметром AD
. Точка B
лежит на окружности с диаметром AC
, поэтому \angle ABC=90^{\circ}
. Аналогично \angle ABD=90^{\circ}
.
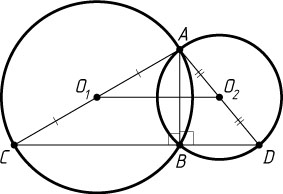
Рассмотрим случай, когда точки O_{1}
и O_{2}
лежат по разные стороны от прямой AB
(рис. 1). Тогда
\angle CBD=\angle ABC+\angle ABD=90^{\circ}+90^{\circ}=180^{\circ},
значит, точки C
, B
и D
лежат на одной прямой, причём точка B
лежит между C
и D
, поэтому CD=BC+BD=a+b
, а так как O_{1}O_{2}
— средняя линия треугольника ACD
, то
O_{1}O_{2}=\frac{1}{2}CD=\frac{a+b}{2}.
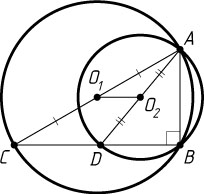
Пусть теперь точки C
и D
лежат по одну сторону о прямой AB
и a\gt b
(рис. 2). Тогда точки B
, C
и D
лежат на одной прямой, причём точка C
лежит между B
и D
. Следовательно,
O_{1}O_{2}=\frac{1}{2}CD=\frac{1}{2}(BD-BC)=\frac{a-b}{2}.
Аналогично для случая a\lt b
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 10.5, с. 76

