3379. В угол вписаны касающиеся внешним образом окружности радиусов r
и R
(r\lt R
). Первая из них касается сторон угла в точках A
и B
. Найдите AB
.
Ответ. \frac{4r\sqrt{Rr}}{R+r}
.
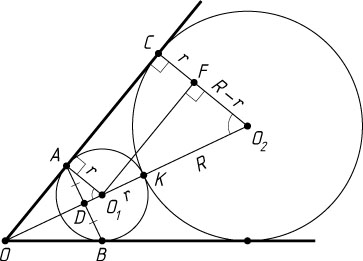
Решение. Пусть меньшая окружность с центром O_{1}
касается сторон угла с вершиной O
в точках A
и B
, большая окружность с центром O_{2}
касается луча OA
в точке C
, а меньшей окружности — в точке K
.
Линия центров двух касающихся окружностей проходит через их точку касания, поэтому
O_{1}O_{2}=KO_{1}+KO_{2}=r+R.
Опустим перпендикуляр O_{1}F
из центра меньшей окружности на радиус O_{2}C
большей окружности. Тогда O_{1}ACF
— прямоугольник, поэтому
O_{2}F=O_{2}C-FC=O_{2}C-O_{1}A=R-r.
Из прямоугольного треугольника O_{1}FO_{2}
находим, что
O_{1}F=\sqrt{O_{1}O_{2}^{2}-O_{2}F^{2}}=\sqrt{(R+r)^{2}-(R-r)^{2}}=2\sqrt{Rr}.
Пусть луч OO_{1}
(биссектриса угла AOC
) пересекает отрезок AB
в точке D
. Тогда AB\perp OO_{1}
, D
— середина AB
и
\angle AO_{1}D=90^{\circ}-\angle FO_{1}O_{2}=\angle O_{1}O_{2}F,
поэтому прямоугольные треугольники AO_{1}D
и O_{1}O_{2}F
подобны, значит, \frac{AD}{O_{1}F}=\frac{AO_{1}}{O_{1}O_{2}}
, или \frac{AD}{2\sqrt{Rr}}=\frac{r}{R+r}
, откуда находим, что AD=\frac{2r\sqrt{Rr}}{R+r}
. Следовательно, AB=2AD=\frac{4r\sqrt{Rr}}{R+r}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.14, с. 112
