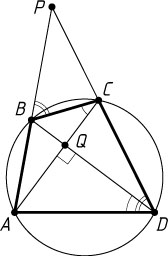
3381. Диагонали AC
и BD
вписанного в окружность четырёхугольника пересекаются в точке Q
под прямым углом. Прямые AB
и CD
пересекаются в точке P
. Известно, что BC=5
, AD=10
, BQ=3
. Найдите AP
.
Ответ. \frac{20\sqrt{5}}{3}
.
Решение. Из прямоугольного треугольника BQC
находим, что
CQ=\sqrt{BC^{2}-BQ^{2}}=\sqrt{25-9}=4.
Прямоугольные треугольники AQD
и BQC
подобны с коэффициентом \frac{AD}{BC}=\frac{10}{5}=2
, поэтому
AQ=2BQ=2\cdot3=6,~DQ=2CQ=2\cdot4=8.
По теореме Пифагора
AB=\sqrt{BQ^{2}+AQ^{2}}=\sqrt{9+36}=3\sqrt{5},~CD=\sqrt{CQ^{2}+DQ^{2}}=\sqrt{16+64}=4\sqrt{5}.
Треугольник BPC
подобен треугольнику DPA
по двум углам, так как
\angle PBC=180^{\circ}-\angle ABC=\angle ADC=\angle ADP,
причём коэффициент подобия равен \frac{BC}{AD}=\frac{5}{10}=\frac{1}{2}
, значит,
CP=\frac{1}{2}AP,~BP=\frac{1}{2}PD=\frac{1}{2}(PC+CD)=\frac{1}{2}\left(\frac{1}{2}AP+4\sqrt{5}\right),
а так как BP=AP-AB=AP-3\sqrt{5}
, то
\frac{1}{2}\left(\frac{1}{2}AP+4\sqrt{5}\right)=AP-3\sqrt{5},
откуда находим, что AP=\frac{20\sqrt{5}}{3}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Задача 4 из диагностической работы 6.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4, с. 169
