3389. Точки D
и E
расположены на стороне AC
треугольника ABC
. Прямые BD
и BE
разбивают медиану AM
треугольника ABC
на три равных отрезка. Найдите площадь треугольника BDE
, если площадь треугольника ABC
равна 1.
Ответ. 0,3.
Указание. Через вершину B
проведите прямую, параллельную AC
.
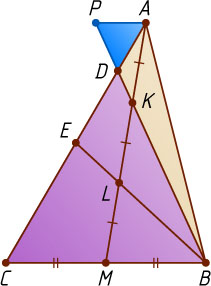
Решение. Пусть прямые BD
и BE
пересекают медиану AM
в точках K
и L
соответственно, причём точка K
лежит между A
и L
, AK=KL=LM
. Точка L
лежит на медиане треугольника и делит её в отношении AL:LM=2:1
, значит, L
— точка пересечения медиан треугольника, поэтому BE
— также медиана. Следовательно, E
— середина стороны AC
.
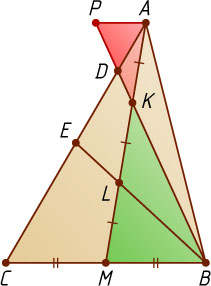
Через вершину A
проведём прямую, параллельную стороне BC
. Пусть эта прямая пересекается с продолжением отрезка BD
в точке P
. Треугольник AKP
подобен треугольнику MKB
с коэффициентом \frac{AK}{KM}=\frac{1}{2}
, поэтому AP=\frac{1}{2}BM=\frac{1}{4}BC
. Треугольник ADP
подобен треугольнику CDB
, значит,
\frac{AD}{DC}=\frac{AP}{BC}=\frac{\frac{1}{4}BC}{BC}=\frac{1}{4},
поэтому
AD=\frac{1}{5}AC,~DE=AE-AD=\frac{1}{2}AC-\frac{1}{5}AC=\frac{3}{10}AC.
Следовательно,
S_{\triangle BDE}=\frac{DE}{AC}\cdot S_{\triangle ABC}=\frac{3}{10}\cdot1=\frac{3}{10}.
