3390. Сторона треугольника равна \sqrt{2}
, углы, прилежащие к ней, равны 75^{\circ}
и 60^{\circ}
. Найдите отрезок, соединяющий основания высот, проведённых из вершин этих углов.
Ответ. 1.
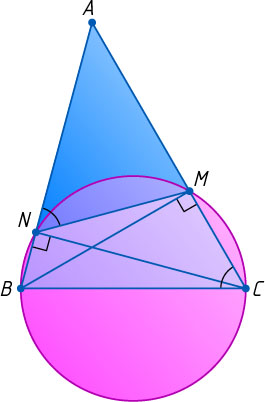
Решение. Пусть BM
и CN
— высоты треугольника ABC
, \angle ABC=75^{\circ}
, \angle ACB=60^{\circ}
. Тогда
\angle BAC=180^{\circ}-75^{\circ}-60^{\circ}=45^{\circ}.
Из точек M
и N
сторона BC
видна под прямым углом, значит, эти точки лежат на окружности с диаметром BC
. Четырёхугольник BCMN
— вписанный, поэтому
\angle ACB=\angle MCB=180^{\circ}-\angle BNM=\angle ANM,
значит, треугольник AMN
подобен треугольнику ABC
по двум углам (угол при вершине A
— общий), причём коэффициент подобия равен
\frac{AM}{AB}=\cos\angle BAM=\cos45^{\circ}=\frac{1}{\sqrt{2}}.
Следовательно,
MN=BC\cdot\frac{1}{\sqrt{2}}=\sqrt{2}\cdot\frac{1}{\sqrt{2}}=1.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.1, с. 122
