3392. Равносторонний треугольник со стороной 3 вписан в окружность. Точка D
лежит на окружности, причём хорда AD
равна \sqrt{3}
. Найдите хорды BD
и CD
.
Ответ. \sqrt{3}
, 2\sqrt{3}
или 2\sqrt{3}
, \sqrt{3}
.
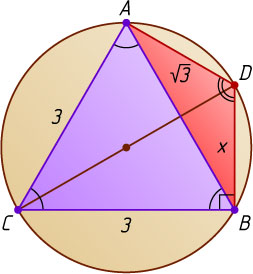
Решение. Пусть точка D
лежит на меньшей дуге AB
(рис. 1). Тогда четырёхугольник ADBC
— вписанный, поэтому
\angle ADB=180^{\circ}-\angle ACB=180^{\circ}-60^{\circ}=120^{\circ}.
Обозначим BD=x
. По теореме косинусов
AB^{2}=AD^{2}+BD^{2}-2AD\cdot BD\cos120^{\circ},
или 9=3+x^{2}+x\sqrt{3}
, откуда находим, что BD=x=\sqrt{3}=AD
, а так как CA=CB
— то прямая CD
— серединный перпендикуляр к хорде AB
, значит, CD
— диаметр окружности. Следовательно, CD=2\sqrt{3}
.
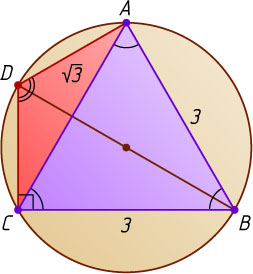
Если же точка D
лежит на меньшей дуге AC
(рис. 2), то аналогично найдём, что BD=2\sqrt{3}
и CD=\sqrt{3}
.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1971, № 5, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.15, с. 87

