3393. Проекция боковой стороны равнобедренной трапеции на большее основание равна a
, средняя линия трапеции равна b
, а острый угол при основании равен 45^{\circ}
. Найдите радиус окружности, описанной около трапеции.
Ответ. \sqrt{\frac{a^{2}+b^{2}}{2}}
.
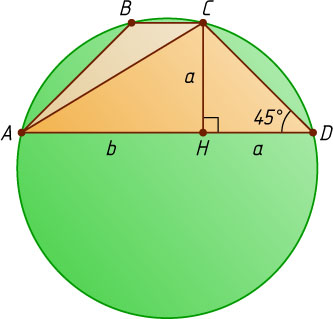
Решение. Пусть ABCD
— равнобедренная трапеция с основаниями AD\gt BC
, \angle ADC=45^{\circ}
, CH
— высота трапеции, R
— радиус окружности, описанной около трапеции. Известно, что проекция диагонали равнобедренной трапеции на большее основание равна полусумме оснований, т. е. средней линии трапеции. Тогда
CH=DH=a,~AH=\frac{1}{2}(AD+BC)=b,~AC=\sqrt{CH^{2}+AH^{2}}=\sqrt{a^{2}+b^{2}}.
Окружность, описанная около трапеции совпадает с окружностью, описанной около треугольника ACD
. По теореме синусов
R=\frac{AC}{2\sin\angle ADC}=\frac{AC}{2\sin45^{\circ}}=\frac{\sqrt{a^{2}+b^{2}}}{2\cdot\frac{\sqrt{2}}{2}}=\sqrt{\frac{a^{2}+b^{2}}{2}}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.9, с. 86
