3394. Найдите радиусы описанной, вписанной и вневписанных окружностей треугольника со сторонами 13, 13, 10.
Ответ. \frac{169}{24}
, \frac{10}{3}
, \frac{15}{2}
, 12, 12.
Решение. Пусть стороны AB
, AC
и BC
треугольника ABC
равны 13, 13 и 10 соответственно, AH
— высота треугольника, R
и r
— радиусы соответственно описанной и вписанной окружностей, r_{a}
, r_{b}
и r_{c}
— радиусы вневписанных окружностей, касающихся сторон BC
, AC
и AB
— соответственно.
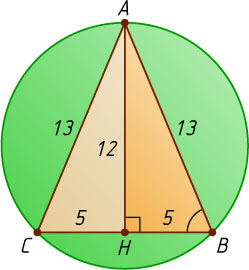
Поскольку треугольник равнобедренный, точка H
— середина основания BC
(рис. 1). Из прямоугольного треугольника ABH
находим, что
AH=\sqrt{AB^{2}-BH^{2}}=\sqrt{13^{2}-5^{2}}=12,~\sin\angle ABC=\sin\angle ABH=\frac{AH}{AB}=\frac{12}{13}.
По теореме синусов
R=\frac{AC}{2\sin\angle ABC}=\frac{13}{2\cdot\frac{12}{13}}=\frac{169}{24}.
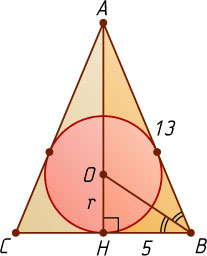
Пусть O
— центр вписанной окружности треугольника ABC
(рис. 2). Тогда BO
— биссектриса треугольника ABH
, поэтому
\frac{OH}{OA}=\frac{BH}{AB}=\frac{5}{13},~\frac{OH}{AH}=\frac{5}{5+13}=\frac{5}{18}.
Следовательно,
r=OH=\frac{5}{18}AH=\frac{5}{18}\cdot12=\frac{10}{3}.
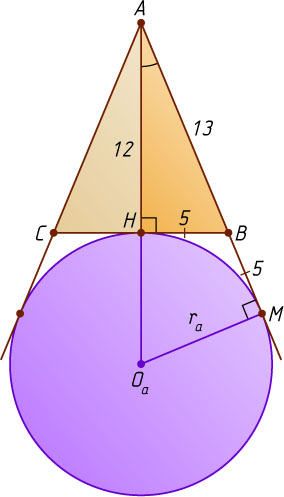
Пусть O_{a}
— центр вневписанной окружности, касающейся стороны BC
и продолжения сторон AC
и AB
, причём продолжения стороны AB
— в точке M
(рис. 3). Тогда
BM=BH=5,~AM=AB+BM=AB+BH=13+5=18.
Из прямоугольного треугольника AMO_{a}
находим, что
r_{a}=O_{a}M=AM\tg\angle MAH=AM\cdot\frac{BH}{AH}=18\cdot\frac{5}{12}=\frac{15}{2}.
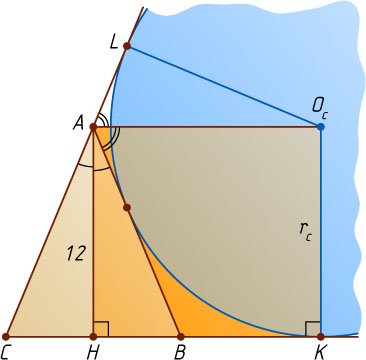
Пусть O_{c}
— центр вневписанной окружности, касающейся стороны AB
и продолжений сторон BC
и AC
в точках K
и L
соответственно (рис. 4). Тогда AO_{c}
— биссектриса угла BAL
, а так как AH
— биссектриса смежного с ним угла BAC
, то \angle HAO_{c}=90^{\circ}
. Четырёхугольник AO_{c}KH
— прямоугольник (\angle HAO_{c}=\angle AHK=\angle HKO_{c}=90^{\circ}
), поэтому
r_{c}=O_{c}K=AH=12.
Аналогично найдём, что r_{b}=AH=12
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.6, с. 86



