3396. В прямоугольном треугольнике синус меньшего угла равен \frac{1}{3}
. Перпендикулярно гипотенузе проведена прямая, разбивающая треугольник на две равновеликие части. В каком отношении эта прямая делит гипотенузу?
Ответ. 2:1
.
Решение. Пусть M
— точка на гипотенузе AB
прямоугольного треугольника ABC
, \sin\angle A=\frac{1}{3}
, N
— точка на катете AC
, MN\perp AB
и S_{\triangle AMN}=\frac{1}{2}S_{\triangle ABC}
.
Обозначим, BC=t
. Тогда
AB=\frac{BC}{\sin\angle A}=\frac{t}{\frac{1}{3}}=3t.
Треугольник ANM
подобен треугольнику ABC
с коэффициентом, равным квадратному корню из отношения площадей, т. е. \frac{1}{\sqrt{2}}
, значит, MN=\frac{t}{\sqrt{2}}
.
Из прямоугольного треугольника ANM
находим, что
AN=\frac{MN}{\sin\angle A}=3MN=\frac{3t}{\sqrt{2}},~AM=\sqrt{AN^{2}-MN^{2}}=\sqrt{\frac{9t^{2}}{2}-\frac{t^{2}}{2}}=2t,
поэтому MB=AB-AM=3t-2t=t
. Следовательно,
\frac{AM}{MB}=\frac{2t}{t}=2.
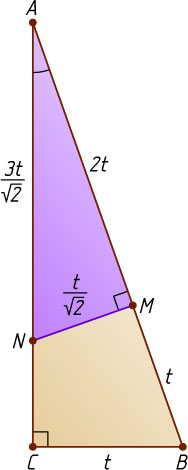
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.20, с. 53
