3397. На медиане AM
треугольника ABC
взята точка K
, причём AK:KM=1:3
. Найдите отношение, в котором прямая, проходящая через точку K
параллельно стороне AC
, делит сторону BC
.
Ответ. 1:7
.
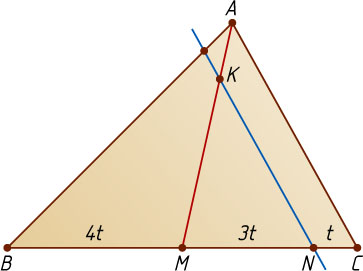
Решение. Пусть прямая, о которой говорится в условии задачи, пересекает сторону BC
в точке N
. Обозначим NC=t
. По теореме о пропорциональных отрезках MN:NC=MK:KA=3:1
, значит,
MN=3NC=3t,~BN=BM+MN=CM+MN=4t+3t=7t.
Следовательно,
\frac{NC}{BN}=\frac{t}{7t}=\frac{1}{7}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.1, с. 46
