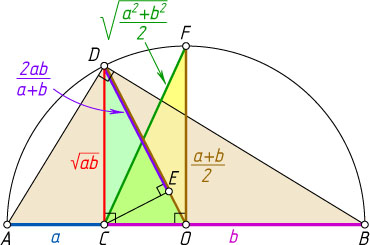
3399. Геометрический смысл классических неравенств. Точка C
лежит на отрезке AB
, причём AC=a
, BC=b
. Перпендикуляры к AB
, восставленные из точки C
и середины O
отрезка AB
, пересекают полуокружность с диаметром AB
в точках D
и F
соответственно, CE
— высота прямоугольного треугольника OCD
. Найдите OD
, CD
, DE
и CF
, и расположите найденные значения по возрастанию.
Ответ. DE=\frac{2ab}{a+b}
, CD=\sqrt{ab}
, OD=\frac{a+b}{2}
, CF=\sqrt{\frac{a^{2}+b^{2}}{2}}
.
Решение. Для определённости будем считать, что a\lt b
.
Точка O
— середина отрезка AB
, поэтому
OD=OF=OA=\frac{AC+BC}{2}=\frac{a+b}{2}.
Отрезок CD
— высота прямоугольного треугольника ADB
, проведённая из вершины прямого угла, поэтому
CD=\sqrt{AC\cdot BC}=\sqrt{ab}.
Отрезок CE
— высота прямоугольного треугольника OCD
, проведённая из вершины прямого угла, поэтому
DE=\frac{CD^{2}}{OD}=\frac{ab}{\frac{a+b}{2}}=\frac{2ab}{a+b}.
По теореме Пифагора из прямоугольного треугольника COF
находим, что
CF=\sqrt{OF^{2}+OC^{2}}=\sqrt{OF^{2}+(OA-AC)^{2}}=\sqrt{\left(\frac{a+b}{2}\right)^{2}+\left(\frac{b-a}{2}\right)^{2}}=\sqrt{\frac{a^{2}+b^{2}}{2}}.
DE
— катет прямоугольного треугольника CED
с гипотенузой CD
, поэтому DE\lt CD
.
CD
— катет прямоугольного треугольника COD
с гипотенузой OD
, поэтому CD\lt OD
.
OF
— катет прямоугольного треугольника COF
с гипотенузой CF
, поэтому OD=OF\lt CF
.
Следовательно, DE\lt CD\lt OD\lt CF
, или
\frac{2ab}{a+b}\lt\sqrt{ab}\lt\frac{a+b}{2}\lt\sqrt{\frac{a^{2}+b^{2}}{2}}.
Примечание. 1. Число \frac{a+b}{2}
называется средним арифметическим чисел a
и b
,
\sqrt{ab}
— средним геометрическим чисел a
и b
,
\frac{2ab}{a+b}
— средним гармоническим чисел a
и b
,
\sqrt{\frac{a^{2}+b^{2}}{2}}
— средним квадратичным (средним квадратическим) чисел a
и b
.
Для любых двух положительных чисел a
и b
верно неравенство
\frac{2ab}{a+b}\leqslant\sqrt{ab}\leqslant\frac{a+b}{2}\leqslant\sqrt{\frac{a^{2}+b^{2}}{2}},
причём равенство достигается тогда и только тогда, когда a=b
.
2. Число \frac{a_{1}+a_{2}+\dots+a_{n}}{n}
называется средним арифметическим чисел a_{1}
, a_{2}
, …, a_{n}
;
\sqrt[{n}]{{a_{1}a_{2}\dots a_{n}}}
— средним геометрическим чисел a_{1}
, a_{2}
, …, a_{n}
;
\frac{n}{\frac{1}{a_{1}}+\frac{1}{a_{2}}+\dots+\frac{1}{a_{n}}}
— средним гармоническим чисел a_{1}
, a_{2}
, …, a_{n}
;
\sqrt{\frac{a_{1}^{2}+a_{2}^{2}+\dots+a_{n}^{2}}{n}}
— средним квадратичным (средним квадратическим) чисел a_{1}
, a_{2}
, …, a_{n}
.
Для любых положительных чисел a_{1}
, a_{2}
, …, a_{n}
верно неравенство
\frac{n}{\frac{1}{a_{1}}+\frac{1}{a_{2}}+\dots+\frac{1}{a_{n}}}\leqslant\sqrt[{n}]{{a_{1}a_{2}\dots a_{n}}}\leqslant\frac{a_{1}+a_{2}+\dots+a_{n}}{n}\leqslant\sqrt{\frac{a_{1}^{2}+a_{2}^{2}+\dots+a_{n}^{2}}{n}},
причём равенство достигается тогда и только тогда, когда a_{1}=a_{2}=\dots=a_{n}
.
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — с. 9
