3406. ABCD
— выпуклый четырёхугольник, в котором AD=BD=AC
. Точки M
и N
— середины сторон AB
и CD
соответственно. Отрезок MN
пересекает диагонали четырёхугольника в точках X
и Y
; P
— точка пересечения AN
и DM
. Докажите, что PX=PY
.
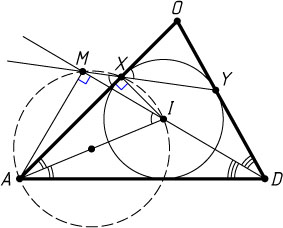
Решение. Первый способ. Докажем сначала следующее утверждение. Если вписанная окружность треугольника AOD
касается сторон OA
и OD
в точках X
и Y
, а биссектриса угла D
пересекается с прямой XY
в точке M
, то \angle AMD=90^{\circ}
. Действительно, если I
— центр вписанной окружности треугольника AOD
, а точка M
лежит на продолжении отрезка XY
за точку X
(рис. 1), то
\angle AXM=\angle OXY=\frac{1}{2}(180^{\circ}-180^{\circ}+\angle OAD+\angle ODA)=
=\angle DAI+\angle ADI=\angle AIM.
Отрезок AM
виден из точек X
и I
под одним и тем же углом, значит, точки A
, M
, X
и I
лежат на одной окружности, а так как \angle AXI=90^{\circ}
, то AI
— диаметр этой окружности. Следовательно, \angle AMD=90^{\circ}
. Аналогично для случая, когда точка M
, лежит на отрезке XY
. Утверждение доказано.
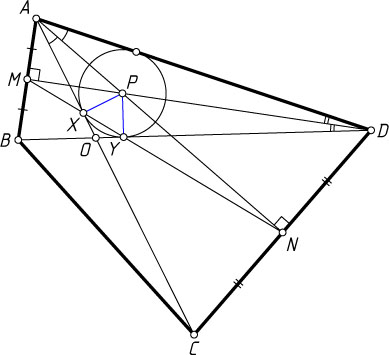
Перейдём к нашей задаче. Пусть диагонали четырёхугольника ABCD
пересекаются в точке O
(рис. 2). Заметим, что в равнобедренных треугольниках ADB
и DAC
медианы DM
и AN
являются биссектрисами и высотами. Значит, во-первых, точка P
— центр вписанной окружности треугольника AOD
, во-вторых, прямая MN
пересекает стороны OA
и OD
в точках касания этих сторон с вписанной окружностью треугольника AOD
. Следовательно, PX=PY
. Что и требовалось доказать.
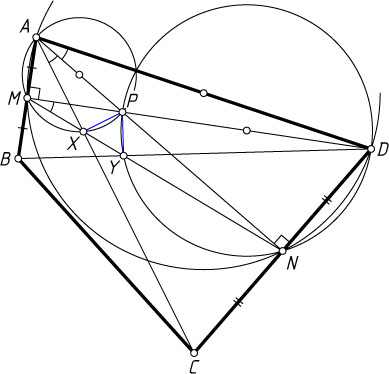
Второй способ. В равнобедренных треугольниках ADB
и CAD
медианы DM
и AN
являются высотами, поэтому из точек M
и N
отрезок AD
виден под прямым углом. Значит, точки M
и N
лежат на окружности с диаметром AD
(рис. 3). Вписанные в эту окружность углы NMD
и NAD
опираются на одну и ту же дугу, поэтому
\angle XMP=\angle NMD=\angle NAD=\angle NAC=\angle PAX.
Значит, из точек M
и A
отрезок PX
виден под одним и тем же углом. Следовательно, точки A
, M
, X
и P
лежат на одной окружности, а так как \angle AMP=90^{\circ}
, то AP
— диаметр этой окружности. По теореме синусов
PX=AP\sin\angle PAX=AP\sin\angle PAD.
Аналогично докажем, что
PY=DP\sin\angle PDY=DP\sin\angle ADP.
Применяя теорему синусов к треугольнику APD
, получим, что \frac{AP}{\sin\angle ADP}=\frac{DP}{\sin\angle PAD}
, или AP\sin\angle PAD=DP\sin\angle ADP
. Следовательно, PX=PY
. Что и требовалось доказать.
Автор: Смирнов А. В.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2007 г., второй тур, 9 класс


