3418. В треугольнике ABC
угол A
в два раза больше угла B
, AL
— биссектриса треугольника. На луче AL
отложен отрезок AK
, равный CL
. Докажите, что AK=CK
.
Решение. Поскольку угол A
вдвое больше угла B
, \angle LAB=\angle LBA
. Значит, треугольник LAB
равнобедренный.
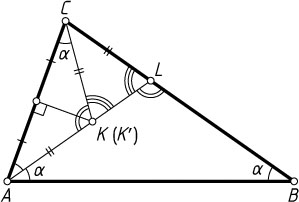
Первый способ. Обозначим \angle CAL=\angle LAB=\alpha
. Поскольку треугольник ALB
равнобедренный, \angle ABL=\angle LAB=\alpha
.
Пусть серединный перпендикуляр к отрезку AC
пересекает луч AL
в точке K'
. Тогда треугольник AK'C
равнобедренный, \angle ACK'=\angle CAK'=\alpha
, AK'=CK'
. Осталось доказать, что AK'=CL
. Тогда точка K'
совпадает с точкой K
.
Пусть точка K'
не совпадает с K
и лежит на отрезке AL
. Тогда LK'C
— внешний угол треугольника ACK'
, поэтому \angle LK'C=2\alpha=\angle CLA
. Значит, треугольник LCK'
равнобедренный и CK'=CL
. Следовательно, AK'=CK'=CL
.
Если же точка K'
лежит на луче AL
вне треугольника ABC
, то
\angle CK'A=180^{\circ}-\angle K'AC-\angle K'CA=180^{\circ}-2\alpha=\angle K'LC.
Значит, треугольник LCK'
равнобедренный, CK'=CL
. Следовательно, AK'=CL
.
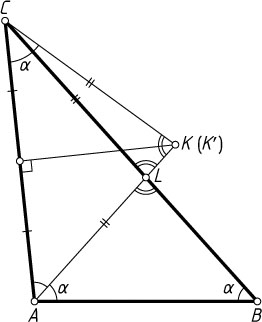
Второй способ. Обозначим \angle CAL=\angle LAB=\alpha
. Поскольку треугольник ALB
равнобедренный, \angle ABL=\angle LAB=\alpha
.
Заметим, что треугольник LAC
подобен треугольнику ABC
по двум углам (\angle LAC=\alpha=\angle ABC
, а угол при вершине C
— общий). Пусть CK'
— биссектриса треугольника LAC
. Тогда треугольник KAC
подобен треугольнику LAB
, значит, \angle ACK'=\angle CAK'=\alpha
, AK'=CK'
.
По теореме о внешнем угле треугольника \angle CK'L=2\alpha
и \angle ALC=2\alpha
, поэтому CL=CK'=AK'
. Значит, точка K'
совпадает с точкой K
. Следовательно, AK=AK'=CK'=CK
. Что и требовалось доказать.
Автор: Берлов С. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2006 г., второй тур, 8 класс

