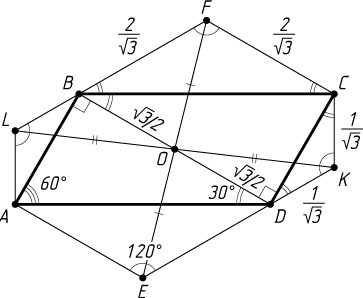
3422. Дан параллелограмм со сторонами 1 и 2 и острым углом 60^{\circ}
. На двух его противоположных сторонах как на основаниях построены вне параллелограмма равнобедренные треугольники с углами 120^{\circ}
при вершинах. Найдите расстояние между этими вершинами.
Ответ. \sqrt{\frac{13}{3}}
; \sqrt{\frac{19}{3}}
.
Решение. Пусть угол при вершине A
параллелограмма ABCD
равен 60^{\circ}
, AB=1
, BC=2
. В равнобедренных треугольниках ADE
и BCF
известно, что
\angle AED=\angle BFC=120^{\circ},~AE=DE=BF=FC=\frac{BC}{\sqrt{3}}=\frac{2}{\sqrt{3}}.
Заметим, что четырёхугольник BEDF
— параллелограмм, так как его противоположные стороны BF
и DE
равны и параллельны. Значит, его диагональ EF
проходит через середину O
диагонали BD
, т. е. через центр параллелограмма ABCD
.
В треугольнике ABD
сторона AB
вдвое меньше стороны AD
, а \angle BAD=60^{\circ}
, поэтому \angle ABD=90^{\circ}
. Тогда
BD=AB\cdot\tg60^{\circ}=1\cdot\sqrt{3}=\sqrt{3},~BO=\frac{1}{2}BD=\frac{\sqrt{3}}{2},
\angle CBD=\angle ABC-\angle ABD=120^{\circ}-90^{\circ}=30^{\circ},
\angle DBF=\angle CBD+\angle CBF=30^{\circ}+30^{\circ}=60^{\circ}.
Из треугольника OBF
по теореме косинусов находим, что
OF=\sqrt{BO^{2}+BF^{2}-2BO\cdot BF\cos60^{\circ}}=\sqrt{\frac{3}{4}+\frac{4}{3}-2\cdot\frac{\sqrt{3}}{2}\cdot\frac{2}{\sqrt{3}}\cdot\frac{1}{2}}=\sqrt{\frac{13}{12}}.
Следовательно,
EF=2OF=2\sqrt{\frac{13}{12}}=\sqrt{\frac{13}{3}}.
Рассмотрим теперь равнобедренные треугольники ALB
и CKD
с углами 120^{\circ}
при вершинах L
и K
. Рассуждая аналогично, докажем, что O
— середина KL
. Из треугольника OKD
по теореме косинусов найдём, что
OK=\sqrt{DO^{2}+DK^{2}-2DO\cdot DK\cos120^{\circ}}=\sqrt{\frac{3}{4}+\frac{1}{3}+2\cdot\frac{\sqrt{3}}{2}\cdot\frac{1}{\sqrt{3}}\cdot\frac{1}{2}}=\sqrt{\frac{19}{12}}.
Следовательно,
KL=2OK=2\sqrt{\frac{19}{12}}=\sqrt{\frac{19}{3}}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.22, с. 25
