3431. Катет и гипотенуза прямоугольного треугольника равны 12 и 20 соответственно. Найдите высоту, проведённую из вершины прямого угла.
Ответ. 9,6.
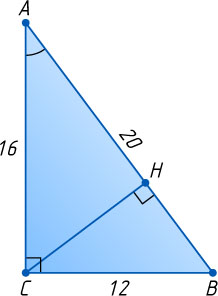
Решение. Пусть ABC
— прямоугольный треугольник с катетом BC=12
и гипотенузой AB=20
, CH
— его высота. По теореме Пифагора
AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{20^{2}-12^{2}}=\sqrt{(20-12)(20+12)}=\sqrt{8\cdot32}=16.
С одной стороны,
S_{\triangle ABC}=\frac{1}{2}AB\cdot CH=\frac{1}{2}\cdot20\cdot CH=10CH,
с другой —
S_{\triangle ABC}=\frac{1}{2}BC\cdot AC=\frac{1}{2}\cdot12\cdot16=96.
Из равенства 10CH=96
находим, что CH=9{,}6
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.1, с. 39
