3432. Найдите высоту прямоугольного треугольника, опущенную на гипотенузу, если известно, что основание этой высоты делит гипотенузу на отрезки, равные 1 и 4.
Ответ. 2.
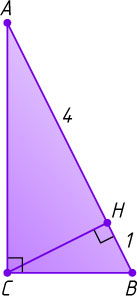
Решение. Пусть ABC
— прямоугольный треугольник с гипотенузой AB
, CH
— его высота, BH=1
, AH=4
.
По теореме о высоте прямоугольного треугольника, проведённой из вершины прямого угла,
CH^{2}=BH\cdot AH=1\cdot4=4.
Следовательно, CH=2
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.2, с. 39
