3433. Высота равнобедренного треугольника, опущенная на боковую сторону, разбивает её на отрезки, равные 2 и 1, считая от вершины треугольника. Найдите основание треугольника.
Ответ. \sqrt{6}
.
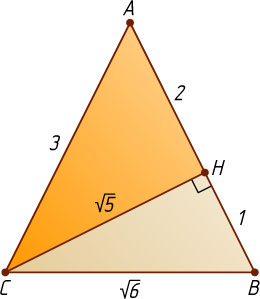
Решение. Пусть CH
— высота равнобедренного треугольника ABC
, опущенная на боковую сторону AB
, AH=2
, BH=1
. Тогда AC=AB=3
.
По теореме Пифагора из прямоугольных треугольников ACH
и BCH
находим, что
CH^{2}=AC^{2}-AH^{2}=9-4=5,~BC^{2}=BH^{2}+CH^{2}=1+5=6.
Следовательно, BC=\sqrt{6}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.3, с. 39
