3436. Диагональ BD
трапеции ABCD
(AD\parallel BC
) разбивает её на два равнобедренных треугольника с основаниями AD
и DC
.
а) Докажите, что луч AC
— биссектриса угла BAD
.
б) Найдите CD
, если известны диагонали трапеции: BD=5
и AC=8
.
Ответ. 6.
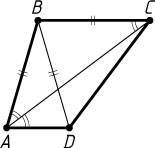
Решение. а) \angle BAC=\angle ACB=\angle CAD
(рис. 1), следовательно, AC
— биссектриса угла BAD
.
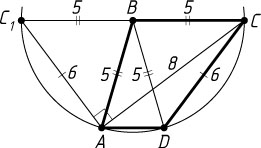
б) Поскольку BA=BD=BC=5
, точки A
, D
и C
лежат на окружности радиуса 5 с центром B
(рис. 2). Продолжим основание BC
за точку B
до пересечения с этой окружностью в точке C_{1}
. Тогда CC_{1}
— диаметр окружности, а ADCC_{1}
— равнобедренная трапеция. Поэтому AC_{1}=CD
, а так как точка A
лежит на окружности с диаметром CC_{1}
, то \angle CAC_{1}=90^{\circ}
. Из прямоугольного треугольника ACC_{1}
находим, что
AC_{1}=\sqrt{CC_{1}^{2}-AC^{2}}=\sqrt{100-64}=6.
Следовательно, CD=AC_{1}=6
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 4.47, с. 41
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4.47.1, с. 50

