3437. В окружность вписаны две трапеции. Основания и боковые стороны одной из них соответственно параллельны основаниям и боковым сторонам другой.
а) Докажите, что диагонали одной трапеции равны диагоналям другой.
б) Найдите отношение площадей этих трапеций, если известно, что боковая сторона одной из них равна радиусу окружности, а боковая сторона другой в два раза меньше.
Ответ. 4:\sqrt{5}
.
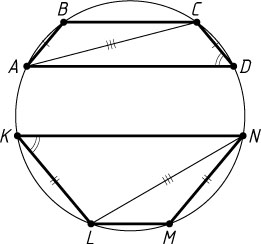
Решение. а) Обе трапеции равнобедренные, так как они вписаны в окружность. Пусть трапеция ABCD
с основаниями AD
и BC
и трапеция KLMN
с основаниями KN
и LM
вписаны в окружность радиуса R
(рис. 1), причём AD\parallel KN
, AB\parallel MN
и CD\parallel KL
. Тогда \angle ADC=\angle LKN
как углы с соответственно сонаправленными сторонами. По теореме синусов AC=2R\sin\angle ADC
и LN=2R\sin\angle LKN
. Следовательно, AC=LN
.
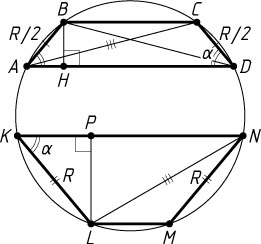
б) Обозначим \angle ADC=\angle LKN=\alpha
(рис. 2). Пусть KL=R
, AB=\frac{R}{2}
. Проведём высоту LP
трапеции KLMN
и высоту BH
трапеции ABCD
. Тогда отрезки NP
и DH
равны средним линиям соответствующих трапеций. Из прямоугольных треугольников KPL
и AHB
находим, что
LP=KL\sin\alpha=R\sin\alpha,~BH=\frac{R}{2}\sin\alpha,
а из прямоугольных треугольников LPN
и BHD
—
NP=\sqrt{LN^{2}-LP^{2}}=\sqrt{4R^{2}\sin^{2}\alpha-R^{2}\sin^{2}\alpha}=R\sqrt{3}\sin\alpha,
DH=\sqrt{BD^{2}-BH^{2}}=\sqrt{4R^{2}\sin^{2}\alpha-\frac{R^{2}}{4}\sin^{2}\alpha}=\frac{1}{2}R\sqrt{15}\sin\alpha.
Проекция диагонали равнобедренной трапеции на основание равна полусумме оснований, т. е. \frac{KN+LM}{2}=NP
и \frac{AD+BC}{2}=DH
. Значит,
S_{KLMN}=NP\cdot LP=R\sqrt{3}\sin\alpha\cdot R\sin\alpha=R^{2}\sqrt{3}\sin^{2}\alpha,
S_{ABCD}=DH\cdot BH=\frac{1}{2}R\sqrt{15}\sin\alpha\cdot\frac{1}{2}R\sin\alpha=\frac{R^{2}}{4}\sqrt{15}\sin^{2}\alpha.
Следовательно,
\frac{S_{KLMN}}{S_{ABCD}}=\frac{R^{2}\sqrt{3}\sin^{2}\alpha}{\frac{R^{2}}{4}\sqrt{15}\sin^{2}\alpha}=\frac{4}{\sqrt{5}}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 4.48, с. 41
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4.49.1, с. 50

