3439. Дан треугольник ABC
со сторонами AB=4
, BC=6
и AC=8
.
а) Докажите, что прямая, проходящая через точку пересечения медиан и центр вписанной окружности, параллельна стороне BC
.
б) Найдите длину биссектрисы треугольника ABC
, проведённой из вершины A
.
Ответ. 2\sqrt{6}
.
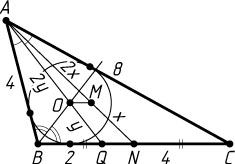
Решение. а) Пусть O
— центр вписанной окружности треугольника ABC
(рис. 1), AN
— медиана треугольника, M
— точка пересечения медиан. Поскольку O
— точка пересечения биссектрис треугольника ABC
, биссектриса AQ
проходит через точку O
. По теореме о биссектрисе \frac{BQ}{CQ}=\frac{AB}{AC}=\frac{4}{8}=\frac{1}{2}
, значит, BQ=\frac{1}{3}BC=2
, а так как BO
— биссектриса треугольника ABQ
, то \frac{AO}{OQ}=\frac{AB}{BQ}=\frac{4}{2}=2
.
Поскольку AN
— медиана треугольника ABC
, то \frac{AM}{MN}=2
. Таким образом, \frac{AO}{OQ}=\frac{AM}{MN}
. Следовательно, OM\parallel BC
.
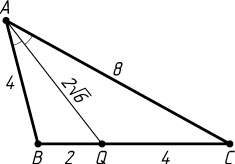
б) По теореме косинусов (рис. 2)
\cos\angle ABC=\frac{AB^{2}+BC^{2}-AC^{2}}{2AB\cdot BC}=\frac{16+36-64}{2\cdot4\cdot6}=-\frac{1}{4}.
Следовательно,
AQ=\sqrt{AB^{2}+BQ^{2}-2AB\cdot BQ\cos\angle ABC}=\sqrt{16+4+2\cdot4\cdot2\cdot\frac{1}{4}}=2\sqrt{6}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 5.30, с. 50
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5.31.1, с. 51

