3440. В параллелограмме ABCD
точка M
— середина стороны AD
, P
— точка пересечения отрезка BM
с диагональю AC
.
а) Докажите, что прямая DP
проходит через середину стороны AB
.
б) Биссектриса угла BAC
пересекает отрезок BM
в точке Q
. Найдите отношение PM:BQ
, если известно, что AB:AC=1:3
.
Ответ. 1:1
.
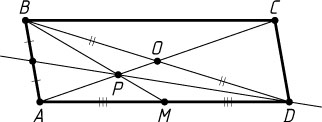
Решение. а) Пусть O
— центр параллелограмма ABCD
(рис. 1). Тогда AO
и BM
— медианы треугольника ABD
, а так как медианы пересекаются в одной точке, то прямая DP
содержит третью медиану. Следовательно, эта прямая проходит через середину стороны AB
.
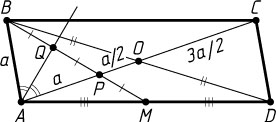
б) Положим AB=a
, AC=3a
(рис. 2). Тогда
AP=\frac{2}{3}AO=\frac{2}{3}\cdot\frac{3}{2}a=a,
значит, биссектриса AQ
равнобедренного треугольника ABP
является его медианой, и
BQ=\frac{1}{2}BP=\frac{1}{2}\cdot\frac{2}{3}BM=\frac{1}{3}BM,
а так как P
— точка пересечения медиан треугольника ABD
, то PM=\frac{1}{3}BM
. Следовательно, \frac{PM}{BQ}=1
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 6.24, с. 58
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6.24.1, с. 59

