3441. Биссектриса AD
треугольника ABC
делит его медиану BM
пополам.
а) Докажите, что площадь треугольника ACD
вдвое больше площади треугольника ABD
.
б) В каком отношении медиана BM
делит биссектрису AD
?
Ответ. 3:1
.
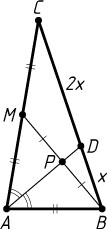
Решение. а) Пусть P
— точка пересечения AD
и BM
(рис. 1). Тогда P
— середина BM
. Медиана AP
треугольника ABM
является его биссектрисой, значит, треугольник ABM
равнобедренный, AB=AM
. Поэтому AC=2AB
. По свойству биссектрисы треугольника
\frac{BD}{CD}=\frac{AB}{AC}=\frac{1}{2}.
Следовательно,
\frac{S_{\triangle ABD}}{S_{\triangle ACD}}=\frac{BD}{CD}=\frac{1}{2}.
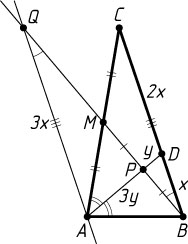
б) Через точку A
проведём прямую, параллельную BC
(рис. 2). Пусть эта прямая пересекается с прямой BM
в точке Q
. Из равенства треугольников AMQ
и CMB
следует, что AQ=BC
, а из подобия треугольников DPB
и APQ
—
\frac{PD}{AP}=\frac{BD}{AQ}=\frac{BD}{BC}=\frac{1}{3}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 6.25, с. 58
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6.26.1, с. 60

