3442. На основаниях AD
и BC
трапеции ABCD
отмечены точки M
и N
соответственно, а на боковых сторонах AB
и CD
— точки K
и L
соответственно. При этом DM:AM=CN:BN=BK:AK=CL:LD=1:2
.
а) Докажите, что четырёхугольник KMLN
— трапеция.
б) Известно, что AD=3BC
. В каком отношении диагональ BD
трапеции ABCD
делит боковые стороны трапеции KMLN
?
Ответ. 2:3
.
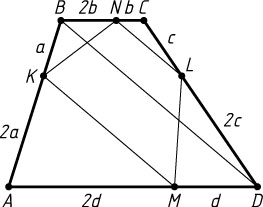
Решение. а) Поскольку \frac{CN}{CB}=\frac{CL}{CD}
, прямая NL
параллельна диагонали BD
(рис. 1). Аналогично прямая KM
также параллельна BD
. Значит, NL\parallel KM
, а так как NL=\frac{1}{3}BD
и KM=\frac{2}{3}BD
, то NL\ne KM
. Следовательно, KMLN
— трапеция.
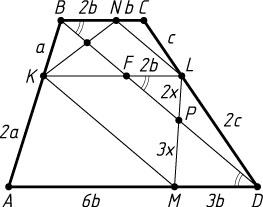
б) Точки L
и K
делят боковые стороны CD
и AB
трапеции ABCD
в одном и том же отношении, значит, KL\parallel AD
(рис. 2). Пусть P
и F
— точки пересечения BD
с ML
и KL
соответственно. Треугольник FDL
подобен треугольнику BDC
с коэффициентом \frac{2}{3}
, поэтому FL=\frac{2}{3}BC
. Треугольник FPL
подобен треугольнику DPM
, поэтому
\frac{LP}{PM}=\frac{FL}{MD}=\frac{\frac{2}{3}BC}{\frac{1}{3}AD}=2\cdot\frac{BC}{AD}=2\cdot\frac{1}{3}=\frac{2}{3},
а так как BD\parallel KM
, то прямая BD
делит боковую сторону AB
трапеции KMLN
в том же отношении.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 6.26, с. 58
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6.27.1, с. 60

