3444. Вневписанная окружность равнобедренного треугольника касается его боковой стороны.
а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание.
б) Известно, что радиус этой окружности в пять раз больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?
Ответ. 1:3
.
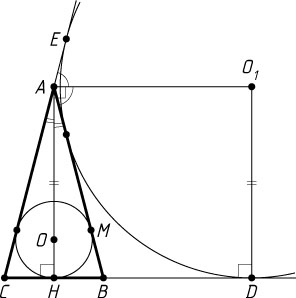
Решение. а) Пусть вписанная окружность с центром O
касается боковой стороны AB
и основания BC
равнобедренного треугольника ABC
в точках M
и H
(рис. 1), а окружность с центром O_{1}
касается боковой стороны AB
, продолжения основания BC
в точке D
и продолжения боковой стороны AC
в точке E
. Тогда AH
— высота треугольника ABC
.
Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому AO_{1}
— биссектриса угла BAE
. В четырёхугольнике AHDO_{1}
угол HAO_{1}
— прямой как угол между биссектрисами смежных углов BAC
и BAE
, а так как \angle HDO_{1}=\angle AHD=90^{\circ}
, то AHDO_{1}
— прямоугольник, поэтому O_{1}D=AH
.
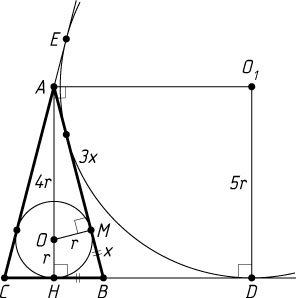
б) Пусть радиус окружности с центром O
равен r
(рис. 2). Тогда радиус окружности с центром O_{1}
равен 5r
.
AH=O_{1}D=5r,~OA=AH-OH=5r-r=4r.
Из прямоугольного треугольника AOM
находим, что
AM=\sqrt{AO^{2}-OM^{2}}=\sqrt{16r^{2}-r^{2}}=r\sqrt{15}.
Прямоугольные треугольники AOM
и ABH
подобны по двум углам, поэтому \frac{AM}{OM}=\frac{AH}{BH}
, откуда
BH=\frac{OM\cdot AH}{AM}=\frac{r\cdot5r}{r\sqrt{15}}=\frac{r\sqrt{15}}{3}.
По теореме об отрезках касательных, проведённых к окружности из одной точки BM=BH=\frac{r\sqrt{15}}{3}
. Следовательно,
\frac{BM}{AM}=\frac{\frac{r\sqrt{15}}{3}}{r\sqrt{15}}=\frac{1}{3}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 6.30, с. 58
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2015
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6.31.1, с. 62

