3446. На диагонали BD
параллелограмма ABCD
отмечены точки P
и Q
, причём BP=PQ=QD
.
а) Докажите, что прямые AP
и AQ
проходят через середины M
и N
сторон BC
и CD
соответственно.
б) Найдите отношение площади пятиугольника CMPQN
к площади параллелограмма ABCD
.
Ответ. \frac{1}{3}
.
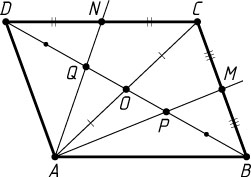
Решение. а) Пусть O
— центр параллелограмма ABCD
(рис. 1). Тогда
BP=\frac{1}{3}BD=\frac{1}{3}\cdot2BO=\frac{2}{3}BO.
Точка P
лежит на медиане BO
треугольника ABC
и делит её в отношении 2:1
, считая от вершины B
, значит, P
— точка пересечения медиан этого треугольника, а тогда медиана AM
проходит через точку P
. Следовательно, прямая AP
проходит через середину BC
. Аналогично прямая AQ
проходит через середину CD
.
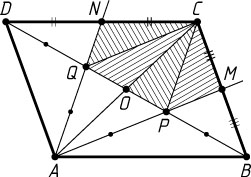
б) Площадь каждого из треугольников ABM
и ADN
равна четверти площади параллелограмма. Площадь треугольника APQ
равна трети площади треугольника ABD
, т. е. шестой части площади параллелограмма. Значит,
S_{CMPQN}=S_{ABCD}-S_{\triangle ABM}-S_{\triangle ADN}-S_{\triangle APQ}=
=S_{ABCD}-\frac{1}{4}S_{ABCD}-\frac{1}{4}S_{ABCD}-\frac{1}{6}S_{ABCD}=\frac{1}{3}S_{ABCD}.
Следовательно, \frac{S_{CMPQN}}{S_{ABCD}}=\frac{1}{3}
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 7.36, с. 67
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 7.36.1, с. 71

