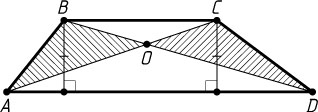
3450. Диагонали AC
и BD
четырёхугольника ABCD
пересекаются в точке O
. Треугольники AOB
и COD
равновелики.
а) Докажите, что BC\parallel AD
.
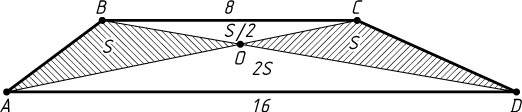
б) Найдите площади треугольников, на которые диагонали разбивают четырёхугольник ABCD
, если известно, что его площадь равна 27, BC=8
, AD=16
.
Ответ. 3, 12, 6, 6.
Решение. а) Треугольники ABD
и ACD
равновелики (рис. 1), так как
S_{\triangle ABD}=S_{\triangle AOB}+S_{\triangle AOD}=S_{\triangle COD}+S_{\triangle AOD}=S_{\triangle ACD}.
Поскольку AD
— общая сторона этих треугольников, то высоты опущенные на эту сторону, равны. Следовательно, прямые BC
и AD
параллельны.
б) Обозначим S_{\triangle AOB}=S_{\triangle COD}=S
(рис. 2). Треугольник BOC
подобен треугольнику DOA
с коэффициентом \frac{1}{2}
, значит,
\frac{OC}{OA}=\frac{1}{2},~\frac{S_{\triangle BOC}}{S_{\triangle AOD}}=\left(\frac{1}{2}\right)^{2}=\frac{1}{4},
\frac{S_{\triangle BOC}}{S_{\triangle AOB}}=\frac{OC}{OA}=\frac{1}{2}.
Значит,
S_{\triangle BOC}=\frac{1}{2}S,~S_{\triangle AOD}=4S_{\triangle BOC}=2S,
а так как 2S+\frac{1}{2}S+4S=27
, то S=6
. Следовательно,
S_{\triangle AOB}=S_{\triangle COD}=6,~S_{\triangle BOC}=3,~S_{\triangle AOD}=12.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 7.41, с. 68
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 7.41.1, с. 73

