3453. Общие внутренние касательные к двум окружностям перпендикулярны. Одна из них касается окружностей в точках A
и C
, вторая — в точках B
и D
(точки A
и B
лежат на одной окружности).
а) Докажите, что отрезок AC
равен сумме радиусов окружностей.
б) Найдите площадь четырёхугольника ABCD
, если известно, что AB=6
, CD=8
.
Ответ. 49.
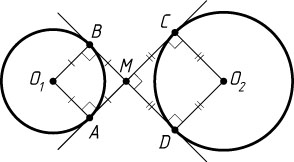
Решение. а) Пусть перпендикулярные прямые AC
и BD
пересекаются в точке M
и касаются окружности с центром O_{1}
в точках A
и B
(рис. 1), а окружности с центром O_{2}
— в точках C
и D
. Четырёхугольники AMBO_{1}
и CMDO_{2}
— квадраты, поэтому AM=O_{1}B
и CM=O_{2}D
. Следовательно, AC=AM+CM=O_{1}B+O_{2}D
.
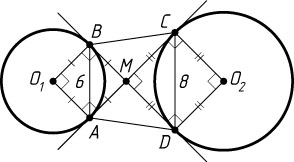
б) Из прямоугольных равнобедренных треугольников AMB
и CMD
(рис. 2) находим, что
AM=\frac{AB}{\sqrt{2}}=\frac{6}{\sqrt{2}},~CM=\frac{CD}{\sqrt{2}}=\frac{8}{\sqrt{2}},
значит,
BD=AC=AM+CM=\frac{8}{\sqrt{2}}+\frac{6}{\sqrt{2}}=\frac{14}{\sqrt{2}}=7\sqrt{2}.
Диагонали AC
и BD
четырёхугольника ABCD
перпендикулярны, следовательно,
S_{ABCD}=\frac{1}{2}AC\cdot BD=\frac{1}{2}\cdot7\sqrt{2}\cdot7\sqrt{2}=49.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 8.29, с. 76
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 8.29, с. 82

