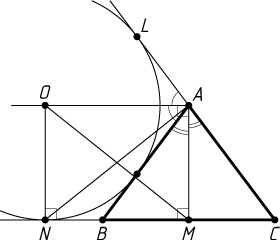
3454. Окружность с центром O
касается боковой стороны AB
равнобедренного треугольника ABC
, продолжения боковой стороны AC
и продолжения основания BC
в точке N
. Точка M
— середина основания BC
.
а) Докажите, что AN=OM
.
б) Найдите OM
, если стороны треугольника ABC
равны 10, 10 и 12.
Ответ. 2\sqrt{41}
.
Решение. а) Пусть L
— точка касания данной окружности с прямой AC
(рис. 1). Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому AO
— биссектриса угла BAL
. Медиана AM
равнобедренного треугольника ABC
является его высотой и биссектрисой. Значит, \angle OAM=90^{\circ}
как угол между биссектрисами смежных углов. Кроме того, \angle AMN=90^{\circ}
и \angle MNO=90^{\circ}
(радиус окружности, проведённый в точку касания, перпендикулярен касательной), поэтому AMNO
— прямоугольник. Диагонали прямоугольника равны, следовательно, AN=OM
.
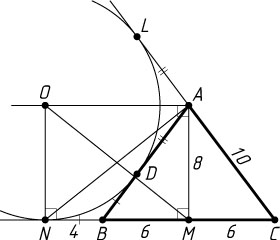
б) По теореме Пифагора из треугольника AMB
находим, что AM=8
(рис. 2). Пусть D
— точка касания данной окружности с боковой стороной AB
треугольника ABC
. Тогда BD=BN
и AD=AL
, значит,
CN+CL=(CB+BN)+(CA+AL)=(CB+BD)+(CA+AD)=
=CB+CA+(BD+AD)=CB+CA+AB=10+12+10=32,
а так как CN=CL
, то CN=\frac{1}{2}\cdot32=16
. Тогда MN=CN-CM=16-6=10
.
Из прямоугольного треугольника AMN
находим что
AN=\sqrt{AM^{2}+MN^{2}}=\sqrt{64+100}=2\sqrt{41}.
Следовательно, OM=AN=2\sqrt{41}
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 8.35, с. 77
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 8.35.1, с. 84

