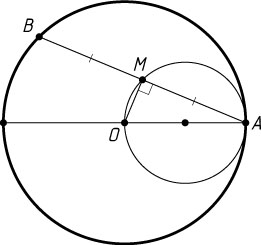
3456. Окружность с центром O
и окружность вдвое меньшего радиуса касаются внутренним образом в точке A
. Хорда AB
большей окружности пересекает меньшую окружность в точке M
.
а) Докажите, что M
— середина AB
.
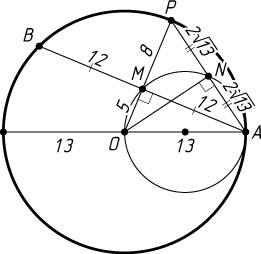
б) Луч OM
пересекает большую окружность в точке P
. Найдите расстояние от центра большей окружности до хорды AP
, если радиус большей окружности равен 13, а OM=5
.
Ответ. 3\sqrt{13}
.
Решение. а) Линия центров касающихся окружностей проходит через точку их касания, поэтому OA
— диаметр меньшей окружности (рис. 1). Если точка M
совпадает с O
, утверждение очевидно. Пусть точка M
отлична от O
. Тогда \angle AMO=90^{\circ}
, так как точка M
лежит на окружности с диаметром OA
. Радиус, перпендикулярный хорде, делит её пополам, следовательно, M
— середина AB
.
б) Из прямоугольных треугольников AOM
и APM
(рис. 2) находим, что
AM=\sqrt{OA^{2}-OM^{2}}=\sqrt{169-25}=12,
AP=\sqrt{AM^{2}+MP^{2}}=\sqrt{12^{2}+(13-5)^{2}}=\sqrt{208}=4\sqrt{13}.
Высота ON
равнобедренного треугольника AOP
является медианой, поэтому AN=\frac{1}{2}AP=2\sqrt{13}
. Следовательно,
ON=\sqrt{OA^{2}-AN^{2}}=\sqrt{169-52}=3\sqrt{13}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 9.49, с. 88
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 9.49.1, с. 95

