3457. Окружности с центрами O_{1}
и O_{2}
касаются внешним образом в точке C
. К окружностям проведены общая внешняя касательная и общая внутренняя касательная. Эти касательные пересекаются в точке D
.
а) Докажите, что треугольник O_{1}DO_{2}
прямоугольный.
б) Найдите радиусы окружностей, если известно, что DO_{1}=\sqrt{5}
и DO_{2}=2\sqrt{5}
.
Ответ. 1 и 4.
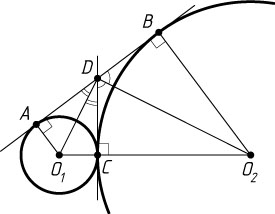
Решение. а) Пусть A
и B
— точки касания окружностей с общей внешней касательной (рис. 1). Точка A
лежит на окружности с центром O_{1}
, точка B
— на окружности с центром O_{2}
. Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому DO_{1}
— биссектриса угла ADC
, а DO_{2}
— биссектриса угла BDC
. Биссектрисы смежных углов перпендикулярны, поэтому \angle O_{1}DO_{2}=90^{\circ}
.
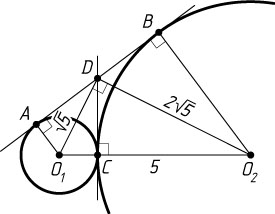
б) Из прямоугольного треугольника O_{1}DO_{2}
(рис. 2) находим, что
OO_{1}=\sqrt{DO_{1}^{2}+DO_{2}^{2}}=\sqrt{5+25}=5.
Линия центров касающихся окружностей проходит через точку их касания, поэтому точка C
лежит на отрезке O_{1}O_{2}
. Тогда DC
— высота прямоугольного треугольника O_{1}DO_{2}
, проведённая из вершины прямого угла. Следовательно, если R_{1}
и R_{2}
— искомые радиусы окружностей, то
R_{1}=O_{1}C=\frac{DO_{1}^{2}}{O_{1}O_{2}}=\frac{5}{5}=1,~R_{2}=O_{2}C=\frac{DO_{2}^{2}}{O_{1}O_{2}}=\frac{20}{5}=4.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 9.50, с. 88
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 9.50.1, с. 95

