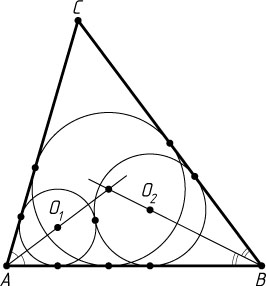
3458. В треугольник ABC
помещены две касающиеся окружности с центрами O_{1}
и O_{2}
, причём первая из них касается сторон AB
и AC
, а вторая — сторон AB
и BC
.
а) Докажите, что прямые AO_{1}
и BO_{2}
пересекаются в центре окружности, вписанной в треугольник ABC
.
б) Найдите радиусы окружностей, если известно, что они равны, а AB=AC=10
и BC=12
.
Ответ. \frac{15}{8}
.
Решение. а) Центр окружности, вписанной в угол, лежит на его биссектрисе, значит, AO_{1}
и BO_{2}
— биссектрисы углов при вершинах A
и B
треугольника ABC
(рис. 1). Следовательно, их точка пересечения — центр вписанной окружности треугольника ABC
.
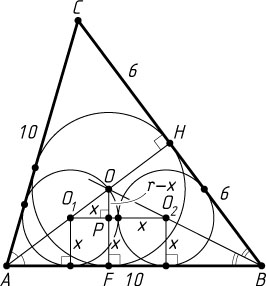
б) Пусть искомый радиус равен x
, радиус вписанной окружности треугольника ABC
равен r
, а биссектрисы углов при вершинах A
и B
треугольника ABC
пересекаются в точке O
— центре вписанной окружности треугольника (рис. 2).
Пусть AH
— высота треугольника ABC
. Треугольник равнобедренный, поэтому H
— середина основания BC
. По теореме Пифагора
AH=\sqrt{AB^{2}-BH^{2}}=\sqrt{100-36}=8,
Значит,
S_{\triangle ABC}=\frac{1}{2}BC\cdot AH=\frac{1}{2}\cdot12\cdot8=48.
В то же время, площадь треугольника равна произведению его полупериметра на радиус вписанной окружности, поэтому r=\frac{48}{10+6}=3
.
Окружности с центрами O_{1}
и O_{2}
равны и касаются, поэтому O_{1}O_{2}\parallel AB
и O_{1}O_{2}=2x
. Треугольник и OO_{1}O_{2}
и OAB
подобны. Пусть высота OF
треугольника OAB
пересекает O_{1}O_{2}
в точке P
. Тогда \frac{OP}{OF}=\frac{O_{1}O_{2}}{AB}
, или \frac{r-x}{r}=\frac{2x}{10}
. Отсюда находим, что x=\frac{5r}{r+5}=\frac{15}{8}
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 9.52, с. 88
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 9.52.1, с. 96

