3461. Окружности, построенные на сторонах AB
и AC
треугольника ABC
как на диаметрах, пересекаются в точке D
, отличной от A
.
а) Докажите, что точка D
лежит на прямой BC
.
б) Найдите угол BAC
, если известно, что \angle ACB=30^{\circ}
, а точка D
лежит на стороне BC
, причём DB:DC=1:3
.
Ответ. 90^{\circ}
.
Решение. а) Точка D
лежит на окружности с диаметром AB
, поэтому \angle ADB=90^{\circ}
. Аналогично \angle ADC=90^{\circ}
.
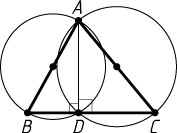
Если точки B
и C
лежат по разные стороны от прямой AD
(рис. 1), то \angle ADB+\angle ADC=180^{\circ}
. Следовательно, точка D
лежит на прямой BC
.
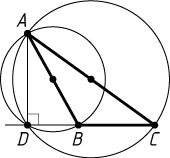
Если же точки B
и C
лежат по одну сторону от прямой AD
(рис. 2), то \angle ADB=\angle ADC
. Следовательно, и в этом случае точка D
лежит на прямой BC
.
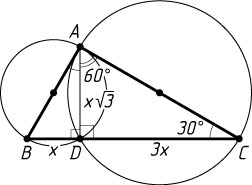
б) Положим BD=x
, CD=3x
. Из прямоугольного треугольника ADC
(рис. 3) находим, что
AD=CD\tg30^{\circ}=3x\cdot\frac{\sqrt{3}}{3}=x\sqrt{3}.
Из прямоугольного треугольника ABD
находим, что
\tg\angle BAD=\frac{BD}{AD}=\frac{x}{x\sqrt{3}}=\frac{\sqrt{3}}{3},
значит, \angle BAD=30^{\circ}
. Следовательно,
\angle BAC=\angle BAD+\angle CAD=30^{\circ}+60^{\circ}=90^{\circ}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 10.14, с. 95
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 10.14.1, с. 103


