3462. Окружность с центром O
вписана в угол, равный 60^{\circ}
. Окружность большего радиуса с центром O_{1}
также вписана в этот угол и проходит через точку O
.
а) Докажите, что радиус второй окружности вдвое больше радиуса первой.
б) Найдите длину общей хорды этих окружностей, если известно, что радиус первой окружности равен 2\sqrt{15}
.
Ответ. 15.
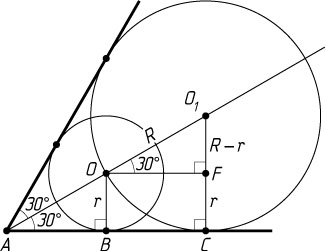
Решение. а) Пусть окружность с центром O
радиуса r
касается одной из сторон угла с вершиной A
в точке B
(рис. 1), а окружность с центром O_{1}
радиуса R\gt r
касается той же стороны в точке C
.
Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому \angle OAB=30^{\circ}
. Пусть F
— проекция точки O
на O_{1}C
. Тогда
OF\parallel AC,~\angle FOO_{1}=\angle OAB=30^{\circ},~FO_{1}=O_{1}C-FC=O_{1}C-OB=R-r.
В прямоугольном треугольнике FOO_{1}
катет FO_{1}
лежит против угла в 30^{\circ}
, значит, OO_{1}=2FO_{1}
, или R=2(R-r)
. Следовательно, R=2r
.
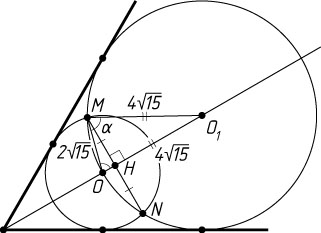
б) Пусть окружности пересекаются в точках M
и N
(рис. 2). Тогда общая хорда MN
окружностей перпендикулярна их линии центров OO_{1}
и делится ею пополам.
Отрезок MH
— высота равнобедренного треугольника OMO_{1}
со сторонами
OM=r=2\sqrt{15},~O_{1}M=2r=4\sqrt{15},~OO_{1}=2r=4\sqrt{15}.
Обозначим \angle MOO_{1}=\angle OMO_{1}=\alpha
. Тогда
\cos\alpha=\frac{MO}{2OO_{1}}=\frac{r}{4r}=\frac{1}{4},~\sin\alpha=\sqrt{1-\cos^{2}\alpha}=\frac{\sqrt{15}}{4},
поэтому
MH=OM\sin\alpha=2\sqrt{15}\cdot\frac{\sqrt{15}}{4}=\frac{15}{2},
Следовательно, MN=2MH=15
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 10.15, с. 95
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 10.15.1, с. 103

