3464. Окружности с центрами O_{1}
и O_{2}
разных радиусов пересекаются в точках A
и B
. Хорда AC
большей окружности пересекает меньшую окружность в точке M
и делится этой точкой пополам.
а) Докажите, что проекция отрезка O_{1}O_{2}
на прямую AC
в четыре раза меньше AC
.
б) Найдите O_{1}O_{2}
, если известно, что радиусы окружностей равны 5 и 17, а AC=16
.
Ответ. 2\sqrt{85}
.
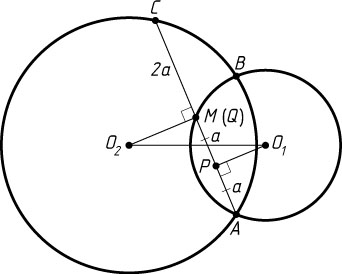
Решение. а) Пусть O_{1}A\lt O_{2}A
, O_{1}P
и O_{2}Q
— перпендикуляры, опущенные из центров окружностей на прямую AC
(рис. 1). Тогда PQ
— проекция отрезка O_{1}O_{2}
эту прямую. Радиус, перпендикулярный хорде, делит её пополам, поэтому P
— середина отрезка AM
, а Q
— середина AC
. Значит, точка Q
совпадает с M
.
Обозначим AP=PM=a
. Тогда MC=AM=2a
, а AC=2MC=4a
. Следовательно, PM=\frac{1}{4}AC
.
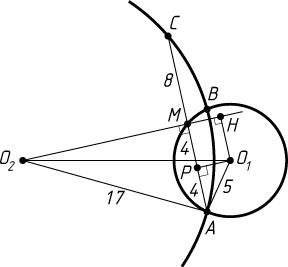
б) В прямоугольных треугольниках AO_{2}M
и AO_{1}P
(рис. 2) известно, что
O_{2}A=17,~AM=\frac{1}{2}AC=8,~O_{1}A=5,~AP=PM=\frac{1}{4}AC=4.
По теореме Пифагора
O_{2}M=\sqrt{O_{2}A^{2}-AM^{2}}=\sqrt{17^{2}-8^{2}}=15,
O_{1}P=\sqrt{O_{1}A^{2}-AP^{2}}=\sqrt{5^{2}-4^{2}}=3.
Опустим перпендикуляр O_{1}H
на прямую O_{2}M
. Тогда HMPO_{1}
— прямоугольник, поэтому
O_{1}H=MP=4,~MH=O_{1}P=3,~O_{2}H=O_{2}M+MH=15+3=18.
Из прямоугольного треугольника O_{1}HO_{2}
находим, что
O_{1}O_{2}=\sqrt{O_{1}H^{2}+O_{2}H^{2}}=\sqrt{4^{2}+18^{2}}=2\sqrt{85}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 10.17, с. 95
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 10.17.1, с. 104

