3467. Дан треугольник со сторонами 25, 25 и 48.
а) Докажите, что он тупоугольный.
б) Найдите расстояние между центрами его вписанной и описанной окружностей.
Ответ. \frac{575}{14}
.
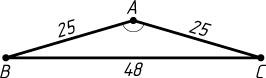
Решение. а) Пусть AB=AC=25
, BC=48
— стороны треугольника ABC
(рис. 1). По теореме косинусов
\angle BAC=\frac{AB^{2}+AC^{2}-BC^{2}}{2AB\cdot AC}=\frac{25^{2}+25^{2}-48^{2}}{2\cdot25\cdot25}=\frac{2\cdot50^{2}-48^{2}}{2\cdot25\cdot25}\lt0.
Следовательно, \angle BAC\gt180^{\circ}
.
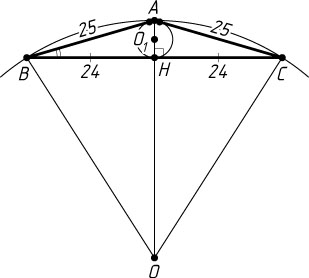
б) Пусть AH
— высота равнобедренного треугольника ABC
(рис. 2). Тогда H
— середина BC
, а так как AH
— биссектриса треугольника, то центр O_{1}
вписанной окружности лежит на отрезке OH
. Поскольку треугольник ABC
тупоугольный с тупым углом при вершине A
, центр O
его описанной окружности и вершина A
лежат по разные стороны от прямой BC
, причём точка O
лежит на серединном перпендикуляре к стороне BC
, т. е. на прямой AH
. Значит, OO_{1}=OA-O_{1}A
.
Из прямоугольного треугольника AHB
находим, что
AH=\sqrt{AB^{2}-BH^{2}}=\sqrt{25^{2}-24^{2}}=7,~\sin\angle ABC=\frac{AH}{AB}=\frac{7}{25},
Пусть OA=R
— радиус описанной окружности треугольника ABC
. По теореме синусов
OA=R=\frac{AC}{2\sin\angle ABC}=\frac{25}{2\cdot\frac{7}{25}}=\frac{625}{14}.
Пусть S
— площадь треугольника ABC
, p
— полупериметр, r=O_{1}H
— радиус вписанной окружности. Тогда
S_{\triangle ABC}=\frac{1}{2}BC\cdot AH=\frac{1}{2}\cdot48\cdot7=24\cdot7,~p=\frac{25+25+48}{2}=49,
r=\frac{S}{p}=\frac{24\cdot7}{49}=\frac{24}{7},~O_{1}A=AH-O_{1}H=AH-r=7-\frac{24}{7}=\frac{25}{7}.
Следовательно,
OO_{1}=OA-O_{1}A=\frac{625}{14}-\frac{25}{7}=\frac{575}{14}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 11.42, с. 109
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 11.41.2, с. 117

