3468. Длины сторон AB
, AD
, BC
и CD
выпуклого четырёхугольника ABCD
в указанном порядке образуют арифметическую прогрессию.
а) Докажите, что в этот четырёхугольник можно вписать окружность.
б) Найдите радиус этой окружности, если известно, что AB=6
, AD=8
, BC=10
, CD=12
и BD=BC
.
Ответ. 4.
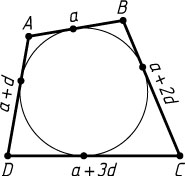
Решение. а) Пусть AB=a
, AD=a+d
, BC=a+2d
, CD=a+3d
(рис. 1). Тогда AB+CD=a+a+3d=2a+3d
и AD+BC=a+d+a+2d=2a+3d
. Значит, AB+CD=AD+BC
. Суммы противоположных сторон выпуклого четырёхугольника ABCD
равны, следовательно, в него можно вписать окружность.
б) Из пункта а) следует, что в данный четырёхугольник можно вписать окружность.
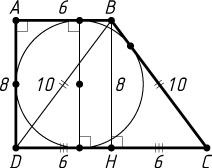
Треугольник ABD
прямоугольный с прямым углом при вершине A
(рис. 2), так как AB^{2}+AD^{2}=36+64=100=BD^{2}
. Треугольник BCD
равнобедренный, его высота BH
является медианой, поэтому
DH=\frac{1}{2}CD=6=AB,~BH=\sqrt{BC^{2}-CH^{2}}=\sqrt{100-36}=8=AD.
Противоположные стороны четырёхугольника ABHD
попарно равны, значит, это параллелограмм, а так как \angle BAD=90^{\circ}
— это прямоугольник. Поскольку AB\parallel CD
, данный четырёхугольник ABCD
— прямоугольная трапеция. Диаметр вписанной в неё окружности равен меньшей боковой стороне AD
. Следовательно, радиус этой окружности равен \frac{1}{2}AD=4
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 11.45, с. 109
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 11.45.1, с. 118

