3470. Сторона AC
треугольника ABC
больше стороны AB
. Вписанная в треугольник окружность касается стороны BC
в точке M
, а вневписанная — в точке N
.
а) Докажите, что MN=AC-AB
.
б) Найдите расстояние между центрами указанных окружностей, если сумма их радиусов равна 24, а MN=10
.
Ответ. 26.
Решение. а) Пусть BC=a
, AC=b
, AB=c
, p=\frac{a+b+c}{2}
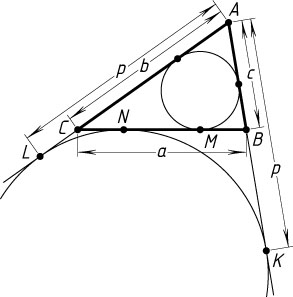
— полупериметр треугольника, а вневписанная окружность касается продолжений сторон AB
и AC
в точках K
и L
соответственно (рис. 1). Тогда
CN=CL,~BN=BK,~AL=AK,
2p=AC+CN+BN+AB=AC+CL+BK+AB=AL+AK=2AL,
поэтому
AL=AK=p=\frac{a+b+c}{2},~CN=CL=AL-AC=p-b=\frac{a+c-b}{2}.
Аналогично докажем, что BM=p-b=\frac{a+c-b}{2}
. Следовательно,
MN=BC-CN-BM=a-\frac{a+c-b}{2}-\frac{a+c-b}{2}=
=a-(a+c-b)=b-c=AC-AB.
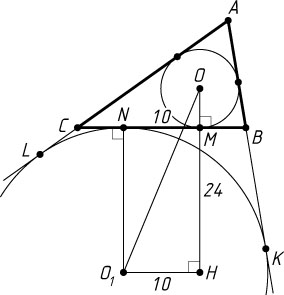
б) Пусть O
—центр вписанной окружности треугольника ABC
(рис. 2), O_{1}
— центр вневписанной окружности, касающейся стороны BC
. Радиусы OM
и O_{1}N
этих окружностей параллельны, так как они перпендикулярны одной и той же прямой BC
.
Пусть H
— основание перпендикуляра, опущенного из точки O_{1}
на прямую OM
. Тогда MNO_{1}H
— прямоугольник, поэтому
HO_{1}=MN=10,~HM=O_{1}N,~OH=OM+HM=OM+O_{1}N=24.
Из прямоугольного треугольника OHO_{1}
находим, что
OO_{1}=\sqrt{HO_{1}^{2}+OH^{2}}=\sqrt{10^{2}+24^{2}}=26.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 11.48, с. 110
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 11.48.1, с. 119

