3471. Диагонали AC
и BD
выпуклого четырёхугольника ABCD
перпендикулярны.
а) Докажите, что AB^{2}+CD^{2}=BC^{2}+AD^{2}
.
б) Известно, что в этот четырёхугольник можно вписать окружность. Найдите её радиус, если BC=8
, CD=12
, \angle BAD=150^{\circ}
.
Ответ. 2,4.
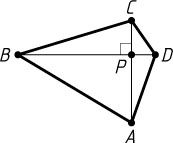
Решение. а) Пусть P
— точка пересечения диагоналей четырёхугольника ABCD
(рис. 1). По теореме Пифагора из прямоугольных треугольников APB
, BPC
, CPD
и APD
находим, что
AB^{2}=PA^{2}+PB^{2},~BC^{2}=PB^{2}+PC^{2},
CD^{2}=PC^{2}+PD^{2},~AD^{2}=PD^{2}+PA^{2}.
Следовательно,
AB^{2}+CD^{2}=(PA^{2}+PB^{2})+(PC^{2}+PD^{2})=
=(PB^{2}+PC^{2})+(PD^{2}+PA^{2})=BC^{2}+AD^{2}.
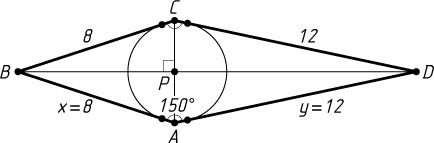
б) Обозначим AB=x
и AD=y
(рис. 2). Поскольку четырёхугольник описанный, то x+12=y+8
, откуда y-x=4
. Диагонали четырёхугольника перпендикулярны, поэтому x^{2}+144=y^{2}+64
, значит, y^{2}-x^{2}=80
, а так как x-y=4
, то x+y=20
. Из системы ~\syst{y-x=4\\y+x=20\\}
находим, что x=8
, y=12
.
Таким образом, четырёхугольник ABCD
разбивается диагональю BD
на два равных треугольника. Тогда
S_{ABCD}=2S_{\triangle ABD}=2\cdot\frac{1}{2}AB\cdot AD\sin150^{\circ}=8\cdot12\cdot\frac{1}{2}=48.
В то же время, площадь описанного четырёхугольника равна произведению его полупериметра на радиус r
вписанной окружности, следовательно,
r=\frac{S_{ABCD}}{AB+AD}=\frac{48}{8+12}=2{,}4.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 11.49, с. 110
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 11.50.1, с. 120

