3472. Точка M
— середина гипотенузы AB
прямоугольного треугольника ABC
. На отрезке CM
как на диаметре построена окружность.
а) Докажите, что она проходит через середины катетов.
б) AP
и BQ
— касательные к этой окружности (P
и Q
— точки касания). Найдите отношение AP:BQ
, если известно, что \tg\angle ABC=2
.
Ответ. 2.
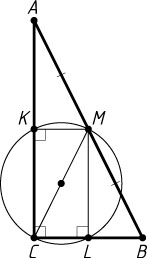
Решение. а) Пусть окружность с диаметром CM
пересекает катеты AC
и BC
прямоугольного треугольника ABC
в точках K
и L
соответственно (рис. 1). Точка K
лежит на окружности с диаметром CM
, поэтому \angle CKM=90^{\circ}
. Прямые KM
и BC
параллельны, так как они перпендикулярны одной и той же прямой AC
. Значит, KM
— средняя линия треугольника ABC
. Следовательно, K
— середина AC
. Аналогично L
— середина BC
.
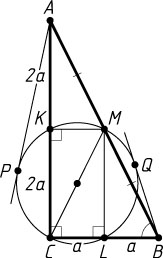
б) Обозначим CL=BL=a
(рис. 2). Тогда
BC=2a,~AC=BC\tg\angle ABC=2a\cdot2=4a,~AK=CK=2a.
По теореме о касательной и секущей
BQ^{2}=BL\cdot BC=a\cdot2a=2a^{2},~AP^{2}=AK\cdot AP=2a\cdot4a=8a^{2},
поэтому
\frac{AP^{2}}{BQ^{2}}=\frac{8a^{2}}{2a^{2}}=4.
Следовательно, \frac{AP}{BQ}=2
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 12.35, с. 118
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 12.35.1, с. 127

