3473. Четырёхугольник ABCD
с перпендикулярными диагоналями AC
и BD
вписан в окружность.
а) Докажите, что прямая, проходящая через точку пересечения диагоналей четырёхугольника перпендикулярно стороне BC
, делит пополам сторону AD
.
б) Найдите стороны четырёхугольника ABCD
, если известно, что AC=84
, BD=77
, а диаметр окружности равен 85.
Ответ. 40, 68, 75, 51.
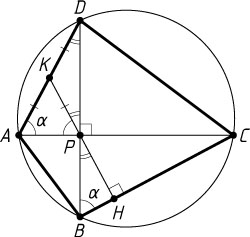
Решение. а) Пусть P
— точка пересечения диагоналей AC
и BD
четырёхугольника ABCD
(рис. 1), PH
— перпендикуляр, опущенный из точки P
на сторону BC
, K
— точка пересечения прямой PH
со стороной AD
. Обозначим \angle DAC=\angle DBC=\alpha
. Тогда
\angle KPD=\angle BPH=90^{\circ}-\alpha,~\angle KDP=90^{\circ}-\alpha=\angle KPD,
\angle APK=90^{\circ}-\angle KPD=90^{\circ}-(90^{\circ}-\alpha)=\alpha.
Значит, треугольники PKD
и PKA
равнобедренные, KA=KP=KD
. Следовательно, K
— середина стороны AD
.
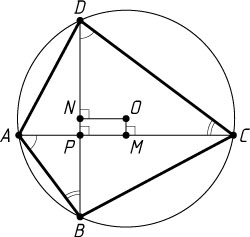
б) Будем считать, что центр O
описанной окружности четырёхугольника ABCD
расположен внутри треугольника CPD
(рис. 2).
Пусть точки M
и N
— проекции точки O
на диагонали AC
и BD
соответственно. Тогда M
и N
— середины диагоналей.
Из прямоугольных треугольников OMC
и OND
находим, что
OM=\sqrt{OC^{2}-MC^{2}}=\sqrt{\left(\frac{85}{2}\right)^{2}-42^{2}}=\sqrt{\left(\frac{85}{2}-42\right)\left(\frac{85}{2}+42\right)}=\sqrt{\frac{1}{2}\cdot\frac{169}{2}}=\frac{13}{2},
ON=\sqrt{OC^{2}-MC^{2}}=\sqrt{\left(\frac{85}{2}\right)^{2}-\left(\frac{77}{2}\right)^{2}}=\sqrt{\left(\frac{85}{2}-\frac{77}{2}\right)\left(\frac{85}{2}+\frac{77}{2}\right)}=\sqrt{\frac{8}{2}\cdot\frac{162}{2}}=18.
Тогда
NP=OM=\frac{13}{2},~BP=BN-NP=\frac{77}{2}-\frac{13}{2}=32,~DP=BD-BP=77-32=45,
MP=ON=18,~AP=AM-MP=42-18=24,~CP=AC-AP=84-24=60.
Из прямоугольных треугольников ABP
и BCP
находим, что
AB=\sqrt{AP^{2}+BP^{2}}=\sqrt{24^{2}+32^{2}}=40,~BC=\sqrt{CP^{2}+BP^{2}}=\sqrt{60^{2}+32^{2}}=68.
Треугольник CPD
подобен треугольнику BPA
с коэффициентом \frac{PC}{PB}=\frac{60}{32}=\frac{15}{8}
, поэтому
CD=\frac{15}{8}AB=\frac{15}{8}\cdot40=75.
Аналогично находим, что
AD=\frac{24}{32}BC=\frac{3}{4}\cdot68=51.
Для любого другого возможного расположения центра O
получим тот же результат.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 12.41, с. 118
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 12.44.1, с. 130

