3474. Отрезок CD
— биссектриса треугольника ABC
. Окружность, проходящая через точки C
и D
касается стороны AB
и пересекает стороны AC
и BC
в точках M
и N
соответственно.
а) Докажите, что MN\parallel AB
.
б) Найдите MN
, если известно, что AD=2
, BD=4
и AM=1
.
Ответ. 4,5
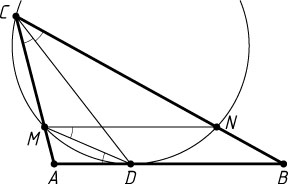
Решение. а) Применяя теорему об угле между касательной и хордой и теорему о вписанных углах, получим (рис. 1), что
\angle ADM=\angle DCM=\angle DCN=\angle DMN.
Следовательно, MN\parallel AB
.
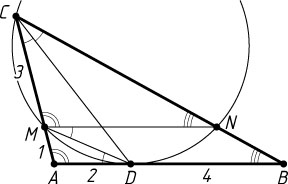
б) По теореме о касательной и секущей AM\cdot AC=AD^{2}
(рис. 2), откуда AC=\frac{AD^{2}}{AM}=\frac{4}{1}=4
. Тогда MC=AC-AM=4-1=3
Поскольку MN\parallel AB
, треугольник CMN
подобен треугольнику CAB
, причём коэффициент подобия равен \frac{CM}{AC}=\frac{3}{4}
. Следовательно,
MN=\frac{3}{4}AB=\frac{3}{4}\cdot(2+4)=\frac{9}{2}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 12.37, с. 118
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 12.37.1, с. 128

