3477. В выпуклом четырёхугольнике ABCD
известно, что \cos\angle ABC=-\cos\angle ADC
.
а) Докажите, что \angle ABD=\angle ACD
.
б) Найдите радиус окружности, описанной около этого четырёхугольника, если известно, что \angle ACB=30^{\circ}
, BC=6
, а высоты треугольников ABD
и CBD
, проведённые из вершины B
, равны.
Ответ. 6.
Решение. а) Из равенства \cos\angle ABC=-\cos\angle ADC
следует, что сумма противоположных углов ABC
и ADC
четырёхугольника ABCD
равна 180^{\circ}
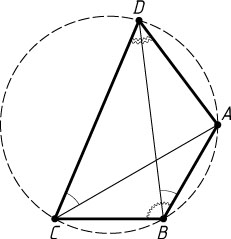
(рис. 1). Значит, около него можно описать окружность. Вписанные в эту окружность углы ABD
и ACD
опираются на одну и ту же дугу, следовательно, они равны.
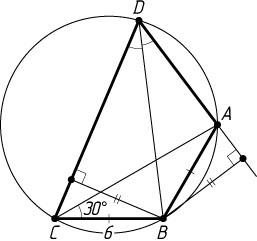
б) Точка B
лежит внутри угла ADC
и равноудалена от его сторон DA
и DC
(рис. 2), значит, DB
— биссектриса этого угла. Поэтому AB=BC=6
. Пусть R
— радиус окружности, описанной около четырёхугольника ABCD
. По теореме синусов
R=\frac{AB}{2\sin\angle ACB}=\frac{6}{2\cdot\sin30^{\circ}}=6.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 13.40, с. 130
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 13.40.1, с. 140

