3479. На основаниях AD
и BC
трапеции ABCD
построены квадраты ADEF
и BCGH
, расположенные вне трапеции.
а) Докажите, что прямая FG
проходит через точку пересечения диагоналей трапеции.
б) Прямая, проходящая через центры квадратов, пересекает основание BC
в точке M
. Найдите BM
, если известно, что BC=20
, AC\perp BD
и BD:AC=3:2
.
Ответ. 12.
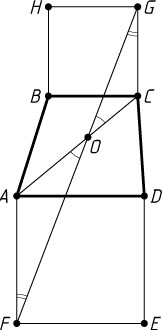
Решение. а) Пусть отрезок FG
пересекает диагональ AC
трапеции в точке O
(рис. 1). Из подобия треугольников AOF
и COG
получаем, что \frac{AO}{OC}=\frac{AF}{CG}=\frac{AD}{BC}
. Но точка пересечения диагоналей делит диагональ AC
том же отношении. Следовательно, O
— точка пересечения диагоналей трапеции.
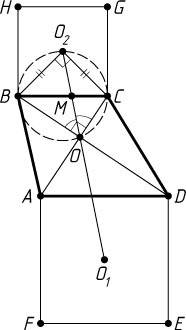
б) Пусть O_{1}
и O_{2}
— центры квадратов ADEF
и BCGH
соответственно (рис. 2). Аналогично предыдущему докажем, что отрезок O_{1}O_{2}
проходит через точку O
пересечения диагоналей трапеции.
Из точек O_{2}
и O
отрезок BC
виден под прямым углом, значит, эти точки лежат на окружности с диаметром BC
. Вписанные в эту окружность углы BOO_{2}
и COO_{2}
опираются на равные хорды, значит, OO_{2}
— биссектриса угла BOC
, а OM
— биссектриса треугольника BOC
. По теореме о биссектрисе треугольника \frac{BM}{MC}=\frac{OB}{OC}
, а так как отрезки OB
и OC
составляют одну и ту же часть соответственно от BD
и AC
, то \frac{OB}{OC}=\frac{BD}{AC}
. Значит, \frac{BM}{MC}=\frac{BD}{AC}=\frac{3}{2}
. Следовательно, BM=\frac{3}{5}BC=\frac{3}{5}\cdot20=12
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 14.41, с. 140
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 14.41.1, с. 151

