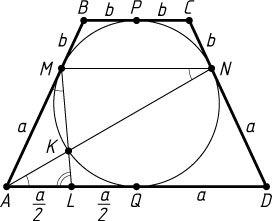
3480. Окружность, вписанная в равнобедренную трапецию ABCD
, касается боковых сторон AB
и CD
в точках M
и N
соответственно. Отрезок AN
пересекает окружность в точке K
, а луч MK
пересекает основание AD
в точке L
.
а) Докажите, что треугольник AKL
подобен треугольнику MAL
.
б) Найдите отношение AL:LD
.
Ответ. 1:3
.
Решение. а) Пусть BC=2b
, AD=2a
, а окружность касается оснований BC
и AD
в точках P
и Q
соответственно. Поскольку трапеция равнобедренная, точки P
и Q
— середины оснований, поэтому
BM=BP=b,~CN=CP=b,~AM=AQ=a,~DN=DQ=a.
Поэтому \frac{BM}{AM}=\frac{b}{a}=\frac{CN}{DN}
, значит, прямая MN
параллельна основаниям трапеции.
Из теоремы об угле между касательной и хордой следует, что
\angle AML=\angle MNK=\angle KAL.
Следовательно, треугольник AKL
подобен треугольнику MAL
по двум углам (угол при вершине L
— общий).
б) Из этого подобия получаем, что \frac{AL}{ML}=\frac{KL}{AL}
, значит, AL^{2}=KL\cdot ML
. По теореме о касательной и секущей LQ^{2}=KL\cdot ML
, поэтому AL=LQ=\frac{1}{2}AQ=b
. Следовательно, \frac{AL}{LD}=\frac{b}{3b}=\frac{1}{3}
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 14.43, с. 140
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 14.43.1, с. 151
