3485. В прямоугольном треугольнике ABC
с гипотенузой AB
проведены медианы AM
и BN
. Известно, что около четырёхугольника ABMN
можно описать окружность.
а) Докажите, что треугольник ABC
равнобедренный.
б) Найдите радиус окружности, описанной около четырёхугольника ABMN
, если также известно, что AB=4\sqrt{5}
.
Ответ. 5.
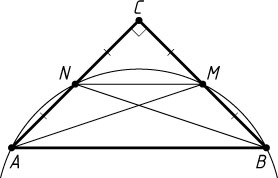
Решение. а) Отрезок MN
— средняя линия треугольника ABC
, поэтому MN\parallel AB
(рис. 1). Поскольку ABMN
— трапеция, вписанная в окружность, она равнобедренная. Значит, AN=BM
. Следовательно, AC=2AN=2BM=BC
.
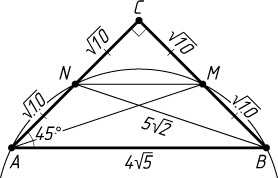
б) Гипотенуза AB
равнобедренного прямоугольного треугольника равна 4\sqrt{5}
, значит, его катеты равны \frac{4\sqrt{5}}{\sqrt{2}}=2\sqrt{10}
(рис. 2). Поэтому NC=\frac{1}{2}BC=\sqrt{10}
. Из прямоугольного треугольника BCN
находим, что
BN=\sqrt{CN^{2}+BC^{2}}=\sqrt{10+40}=5\sqrt{2}.
Пусть R
— радиус окружности, описанной около четырёхугольника ABMN
. По теореме синусов
R=\frac{BN}{2\sin\angle BAN}=\frac{5\sqrt{2}}{2\sin45^{\circ}}=5.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. —

