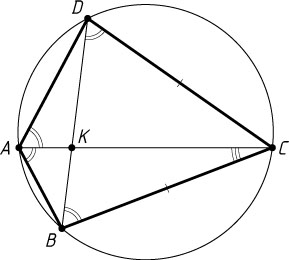
3486. Во вписанном четырёхугольнике ABCD
стороны BC
и CD
равны. Диагонали четырёхугольника пересекаются в точке K
.
а) Докажите, что AC\cdot CK=BC^{2}
.
б) Найдите площадь этого четырёхугольника, если известно, что AC=8
и \angle BAD=150^{\circ}
.
Ответ. 16.
Решение. а) Вписанные углы BAC
и DAC
равны, так как они опираются на равные хорды (рис. 1). Вписанные углы CBD
и CAD
равны, так как они опираются на одну и ту же дугу. Поэтому
\angle CBK=\angle CBD=\angle CAD=\angle BAC.
Значит, треугольники BKC
и ABC
подобны по двум углам (угол при вершине C
— общий), поэтому \frac{CK}{BC}=\frac{BC}{AC}
. Следовательно, AC\cdot CK=BC^{2}
.
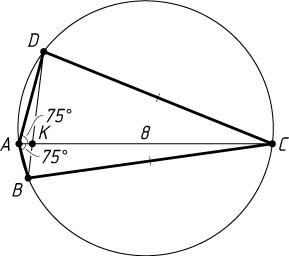
б) AC
— биссектриса угла BAD
(рис. 2), поэтому \angle BAC=\angle DAC=75^{\circ}
. По теореме косинусов
BC^{2}=AB^{2}+AC^{2}-2AB\cdot AC\cos75^{\circ},~CD^{2}=AD^{2}+AC^{2}-2AD\cdot AC\cos75^{\circ}.
Из равенства BC=CD
следует, что
AB^{2}+AC^{2}-2AB\cdot AC\cos75^{\circ}=AD^{2}+AC^{2}-2AD\cdot AC\cos75^{\circ},
откуда находим, что AB+AD=2AC\cos75^{\circ}=16\cos75^{\circ}
. Следовательно,
S_{ABCD}=S_{\triangle ABC}+S_{\triangle ADC}=\frac{1}{2}AB\cdot AC\sin75^{\circ}+\frac{1}{2}AD\cdot AC\sin75^{\circ}=
=\frac{1}{2}AC(AB+AD)\sin75^{\circ}=\frac{1}{2}\cdot8\cdot16\cos75^{\circ}\sin75^{\circ}=32\sin150^{\circ}=32\cdot\frac{1}{2}=16.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 12.43, с. 119
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 12.44.2, с. 130

